1. 서론
다른 우주비행체를 목표로 하는 랑데부/도킹 기술은 궤도상서비싱 임무를 수행하는데 있어 매우 중요한 문제 중 하나이다. 특히 최근 우주 공간상에서 로봇 팔을 이용한 임무들이 생겨 랑데부/도킹 기술이 주목을 받고 있다. 랑데부/도킹은 일반적으로 수동적이고 움직이지 않는 도착(target) 위성과 능동적이고 도착 위성에 도달하기 위해 필요한 기동을 수행하는 출발(chaser) 위성 간의 상대적인 운동에 필요하다. 또한 도착 위성에 해당하는 국제 우주 정거장(ISS)과 출발 위성에 해당하는 우주왕복선이 서로 근접하기 위해 필요한 기술이다. 랑데부/도킹 기술을 이해하기 위해서는 먼저 우주선이 근접할 때 상대적으로 다른 우주선을 조종하는 문제를 이해하기 위해 두 물체 간의 상대운동(two-body problem)을 알아야 한다.
최근 연구에서는 최적의 추력을 고려한 랑데부/도킹을 제어하는 연구[1], 선형화 된 상대운동 방정식과 제한된 추력을 이용한 연구[2], 도착 위성의 궤도가 원형에 가까운 궤도에 관한 연구[3], 공면에서의 랑데부/도킹 제어 연구[4] 등이 있다. 본 논문에서는 도착 위성의 궤도가 기본적인 원 궤도일 때 랑데부/도킹하는 문제를 다룬다.
본 논문은 다음과 같은 구조로 되어 있다. 먼저, 뉴턴의 만유인력을 기반으로 하는 두 물체 간의 상대운동에 대한 방정식을 살펴본 후, 선형화 과정을 거쳐 랑데부/도킹을 위한 방정식을 유도한다. 그리고 적절한 제어기와 중력 섭동을 고려한 시뮬레이션에 대해 분석한다.
2. 본론
우주비행체의 상대운동방정식에서 사용하는 대표적인 좌표계는 지구가 중심인 관성 좌표계(earth centered inertial frame)이다. Fig. 1은 지구 중심 관성 좌표계를 나타낸다. X축은 춘분점(vernal equinox) 방향을 나타내고 XY면은 지구의 적도면(equatorial plane)이며, Z축은 지구의 자전축과 일치하며 북쪽을 가리킨다. Y축은 X축과 Z축을 직교하는 축이다[5].
기본적인 우주비행체의 운동방정식은 뉴턴역학을 기반으로 하는 2체 문제(two-body problem)을 따른다. Fig. 2에서 물체 m2 에 대한 m1 의 힘을 F12, 물체 m1 에 대한 m2 의 힘을 F21 이라 하면 다음과 같다.
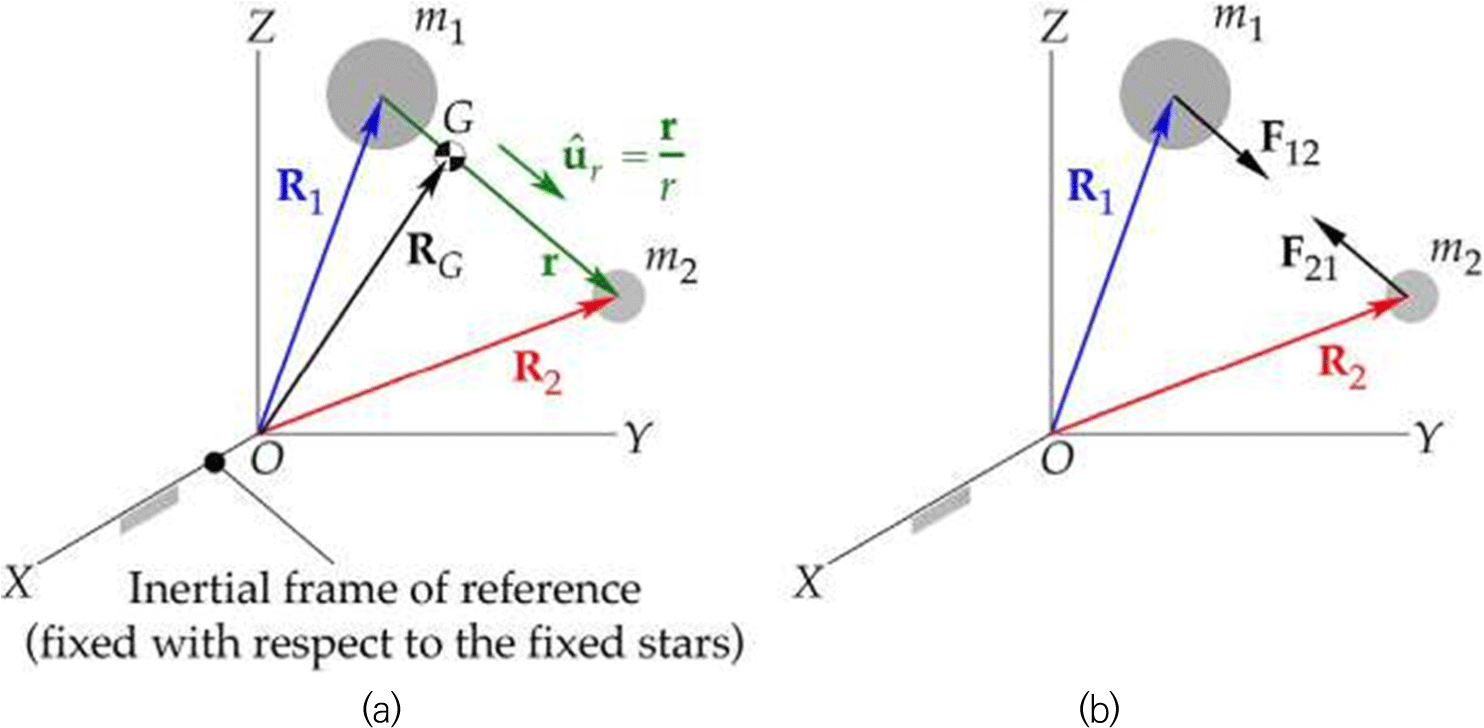
여기서 G 는 두 물체 사이의 무게 중심을, ũr 은 상대 위치 벡터 r 의 단위 벡터를 의미한다. 상대 위치 벡터 r 의 정의의 2계 미분 도함수에 식 (1)을 대입하면 미분방정식의 형태로 표현된 상대운동방정식이 나오게 된다.
여기서 μ 는 표준 중력 변수(standard gravitational parameter)로 G(m1 + m2) 을 의미한다.
식 (2)를 선형화 시킨 후 근접 운용이라는 가정과 도착 위성의 궤도가 원 궤도라는 가정을 대입하면 CW 방정식(Clohessy-Wiltshire equations)을 얻을 수 있다[5].
지구를 포함한 다른 회전하는 천체들은 완벽한 구체가 아닌 살짝 찌그러진 타원형이거나 구형의 구상체를 닮았다. 이러한 행성에서 회전 축은 중력장의 회전 대칭 축이고 원심력에 의한 적도 팽대부에 의해 중력장은 위도와 반지름에 따라 달라진다. 따라서 균일한 중력장 분포를 가지지 않으므로 실제 위성의 운동방정식은 이러한 부분이 고려되어야 한다[6].
중력장은 회전 대칭이기 때문에 방위각에 의존하지 않는다. 따라서 중력 퍼텐셜 에너지(gravitational potential energy)는 다음과 같다.
위성이 지구의 중력장 불균형으로부터 받는 회전 대칭 섭동(rotationally symmetric perturbation)은 지구의 띠 조화 함수(zonal harmonics)와 르장드르 다항식(legendre polynomials)를 이용하면 다음과 같다[7].
여기서 Jk는 행성 주위의 위성 운동의 관측으로부터 추론된 무차원 매개변수이고 중력 불균형으로 궤도에 영향력을 행사하며, 띠 조화 함수라고 부른다. R 은 지구의 적도 반경을, ϕ 는 양의 z축에서 우주비행체의 반경 방향으로 측정한 극 각(polar angle)을 나타내며, Pk 는 르장드르 다항식을 의미한다. k > 6이면 띠 조화 함수가 모두 J2 보다 3배 이상 작아지므로 일반적으로 2차 띠 조화 함수까지 고려한다[7]. 지구의 띠 조화 함수는 Table 1에 정리되어 있다.
| Zonal harmonics | Values |
|---|---|
| J 2 | 1.08263(10−3) |
| J 3 | -2.33936(10−3)J2 |
| J 4 | -1.49601(10−3)J2 |
| J 5 | -0.20995(10−3)J2 |
| J 6 | 0.49941(10−3)J2 |
르장드르 다항식은 로드리게스 함수(Rodrigues’ formula)를 이용하여 얻을 수 있다[8].
2차 띠 조화 함수와 식 (5)를 이용하면 섭동 가속도(perturbing acceleration)식은 다음과 같다.
따라서 식 (3)과 식 (7)를 이용하면 J2 섭동을 고려한 운동방정식이 도출된다.
여기서 n 은 도착 위성 궤도의 평균 운동(mean motion)을, r 은 도착 위성의 위치벡터의 크기를 나타낸다.
본 논문에서 사용한 제어기는 선형 제어기인 PD(proportional-derivative) 제어기를 사용하였다. 운동방정식은 도착 위성의 궤도를 원 궤도라 가정하여 도출한 CW 방정식에 추력 가속도 요소를 추가하고 좌표계는 LOS(line-of-sight) 좌표계로 변환하여 사용하였다. 여기서 LOS 좌표계는 직선거리를 의미하는 ρ 와 랑데부/도킹 방향각을 의미하는 θ 에 대해 표현한다. LOS 좌표계에서 LOS 속도(vρ)와 transverse 속도(vθ)는 다음과 같다.
식 (9)의 시간 도함수에 CW 방정식과 LOS 좌표계에서의 추력 가속도를 더하고 vθ = ρθ˙ 을 시간에 대해 미분하면 LOS 좌표계에서의 가속도와 각가속도에 관한 식이 도출된다. 이 과정에서 비선형 제어기(wρ, wθ)를 얻을 수 있다.
LOS 좌표계에서의 추력 가속도 제어기(aρ, aθ)는 좌표를 변환하는 과정에서 비선형 식을 제거하고 선형 제어기로만 제어하기 위해 선형 제어기와 비선형 제어기로 나누어 표현하였다.
식 (10)과 (11)을 통해 LOS 좌표계에서의 운동방정식을 얻을 수 있다.
따라서 선형 PD 제어기는 다음과 같이 도출된다.
여기서 4개의 게인 값(gain value) k1, k2, k3, k4는 모두 양수이다. 제어 법칙 식 (10)과 (13)가 사용될 때, LOS 프레임의 운동 방정식은 두 개의 선형 2차 미분 방정식으로 변환된다. 따라서 원하는 도킹 축에 대한 수렴이 보장되며 피드백 게인 값을 조정하여 원하는 응답 특성을 얻을 수 있다[9].
선형 시스템과 피드백 제어 법칙에 대한 방정식은 각각 다음과 같이 주어진다.
상태 피드백(state feedback)은 지정된 시스템에 대한 제어 동작을 계산하기 위해 상태 벡터(state vector)를 사용한다. 식 (14)에서 K 는 상태 피드백 게인 값 행렬, A 와 B, C는 선형 시스템을, v(k) 는 기준 입력 벡터를, y 와 u 는 각각 측정된 출력과 제어 입력을 의미한다. 식 (14)의 첫 번째 식과 세 번째 식을 결합하면 폐-루프 상태 방정식을 얻을 수 있다.
식 (15)를 이용하여 식 (14)를 재작성해 보면 다음과 같다.
여기서 cl 은 폐-루프 상태 행렬로써 A-BK 을 의미한다. 폐-루프 시스템은 상태 행렬 cl 의 고유 값(eigenvalue) 및 고유 벡터(eigenvector)에 따라 달라진다. 따라서 게인 값 행렬 K 의 적절한 선택으로 원하는 시스템 역학을 적용할 수 있다[10].
2.3절과 2.4절에서 제안한 feedback control system을 사용하여 랑데부 및 도킹의 수치 시뮬레이션을 진행했다. 제어 법칙에서 CW 좌표가 필요하기 때문에 LOS 좌표(ρ, θ)는 출발 위성과 도착 위성의 위치와 속도를 다르게 하여 계산된다.
본 논문에서 다루고 있는 임무는 비공면(non-coplanar)에서 도착 위성에 해당하는 space station의 궤도가 원 궤도일 때 출발 위성인 spacecraft가 접근하여 랑데부/도킹하는 임무이다. 초기 조건으로 도착 위성과 출발 위성의 위치와 속도가 주어져 있다고 가정한다. 시뮬레이션에 대한 구성은 Table 2와 Table 3에 정리되어 있다.
| Gain values (k1,k2,k3,k4) | 0.7, 0.1, 2.6, 2.1 |
| Desired range | 0.3 km |
| Desired LOS velocity | –0.0002 km/s |
| Desired docking angle | –30° |
이 임무에서 사용되는 초기조건은 다음과 같다. 도착 위성의 초기 위치는 [1622.39, 5305.10, 3717.44]Tkm, 초기 속도는 [-7.29936, 0.492329, 2.48304]Tkm/s이며, 출발 위성의 초기 위치는 [1612.75, 5310.19, 3750.33]Tkm, 초기 속도는 [-7.35170, 0.463828, 2.46906]Tkm/s이다. 근접 운용(proximity operation, PO)을 하기 위해서는 도착 위성과 출발 위성 간의 거리가 비교적 짧은 거리인 0.3 km에서 시작되고 접근 속도는 –0.0002 km/s의 속도로 천천히 접근하는 것이 적절하다고 판단했다. 목표 도킹 각은 처음 45°에서 시작해 충분한 궤적을 그릴 수 있도록 하기 위해 –30°로 설정하였다.
Fig. 3은 3차원에서의 랑데부/도킹 궤도를 보여준다. 근접 운용이 되기 전까지는 높은 추력 가속도로 인해 빠르게 접근 후 PO 지점(0.3 km)에서 적은 속도로 천천히 도달하는 것을 볼 수 있다. Fig. 4와 Fig. 5는 각각 LOS 좌표계에서의 출발 위성과 도착 위성 사이의 거리와 도킹 각을 보여준다. 출발위성이 궤적을 따라 접근을 시작하고 도착 위성에 충분히 접근하면 거리 오차에 관한 피드백 항은 0으로 설정되어 –0.0002 km/s의 속도로 거리가 0으로 수렴하게 되고 이에 따라 도킹 각 또한 목표 값 –30°으로 수렴하게 된다. 출발 위성은 36초 뒤에 도착 위성에 도달하고 목표 방향에 –0.008 km/s의 속도로 도달한다. Fig. 6과 Fig. 7은 각각 LOS 좌표계에서의 거리와 도킹 각의 변화량을 보여주고, Fig. 8은 LOS 좌표계에서의 추력 가속도를 나타낸다.
3. 결론
본 연구에서는 랑데부 및 도킹 기동을 수행하기 위한 피드백 제어 법칙을 사용하고 J2 섭동을 고려하여 원하는 접근 속도로 임의의 고정 도킹 방향을 따라 추적하도록 하였다. 비록 제어 체계는 선형 운동방정식을 기반으로 하며, 비선형 시스템의 시뮬레이션은 선형 시스템보다 정확한 랑데부 및 도킹 조건을 필요로 한다는 것을 보여주지만, 제시한 피드백 제어 법칙은 비교적 간단하므로 자율 도킹 기동을 위한 잠재적인 제어 법칙이 될 것으로 보인다. 또한, 이를 기반으로 비선형 운동방정식 시스템에 적용하면 보다 정교한 자율 도킹이 가능하고 우주 쓰레기 처리, 로봇 팔을 이용한 다양한 임무 등 궁극적으로 궤도상서비싱 임무에 유용하게 활용이 가능할 것이라 사료된다.









