1. 서론
인공위성이 행성탐사 등의 다양한 임무를 수행함에 있어서 자신의 궤도를 파악하여 갱신하는 자율항법이 중요하다. 이를 위해 사용되는 방식으로 크게 레이더 추적 방식과 같은 지구 기반의 수동적 위성 항법, 타 위성 간의 GPS(Global Positioning System) 통신을 이용한 반 능동적 위성 항법이 있다. 하지만 기존 방식의 항법은 지상의 기지국과의 거리가 멀어짐에 따라 위성 항법 오차가 증가한다는 단점이 있다. 지구 센서의 경우에는 인공위성의 지표면으로부터의 고도를 산출하는 데에 이용되지만, 3축에 대한 자세정보를 곧바로 산출할 수 없다는 단점이 있다. 따라서 이러한 문제점을 해결하고자 인공위성의 자율항법을 위해서 지구센서로부터 현재 고도 정보를 획득하고, 별 추적기를 이용하여 국부 수평면 상에서의 위성 자세 정보를 획득하여 활용함으로써 위치를 실시간으로 추정할 수 있다. 다만 지구센서 모의는 불가하므로 위성의 동역학 방정식으로 대체하여 위성의 고도 정보를 획득하였다고 가정하였다. 별 추적기를 이용하여 위성의 자세를 추정하면 대기권의 영향이 희박한 곳에서도 관측할 수 있고, 천체 상에서 위치가 거의 변하지 않기 때문에 가장 신뢰도가 높다.
본 연구에서는 이러한 이유로 위성 자율항법을 구현하기 위해 별 추적기 시뮬레이터를 구성하였다. 2장에서는 시뮬레이터 구성에 대해 기술하고, 3–5장에서는 위성 자율항법을 위한 알고리즘을 3가지로 구분하여 기술하도록 한다. 우선 천구 영상을 별 추적기 시뮬레이터의 CCD(charge-coupled device) 카메라로 획득하여 영상처리를 통해 중심점을 찾아 별을 인식한다. 이로부터 위성이 별을 바라보는 ECI(earth-centered inertial) 좌표계에서의 자세 정보를 획득한다. 최종적으로 위성의 지역 평면과 지구로부터의 고도가 주어졌을 때 위성의 궤도상에서의 위치를 추정하는 과정을 거친다. 시나리오 분석으로 통해 위성 자세 추정 오차는 1도 이내, 위치 추정 오차는 5 km 이내의 성능을 만족하는지 검증하였다.
본 논문에서 수행한 연구를 통해 별 추적기는 실시간으로 천구상의 별 영상을 획득하여 영상처리 및 별 인식, 자세결정 알고리즘을 통해 위성 자율항법에 활용할 수 있고, 추후 알고리즘 개선을 통해 위성 자세 및 위치 오차 수준을 줄일 수 있을 것으로 기대된다.
2. 별 추적기 시뮬레이터 흐름도
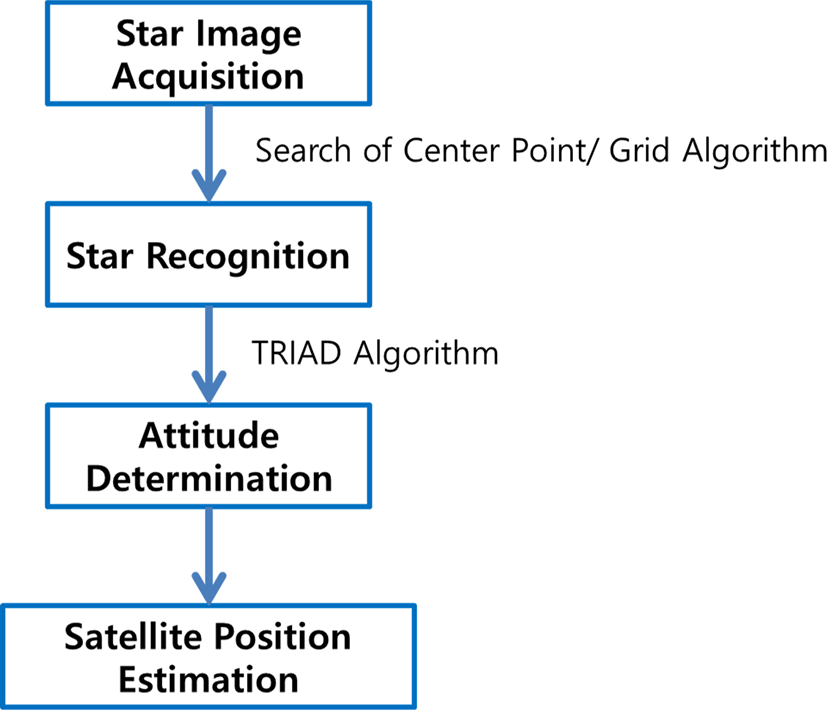
별 추적기 시뮬레이터는 Fig. 1에 도시한 바와 같이 크게 CCD 카메라로 획득한 별 이미지 영상처리를 통한 별 인식, 자세 결정, 위성 위치 추정 단계로 구분할 수 있다[1]. 영상처리 단계에서는 별의 중심점을 찾고, 중심 별과 주변 별들의 패턴을 파악하여 별 인덱스를 산출 후 인식한다. 그 후 TRIAD(Tri-Axial Attitude Determination) 알고리즘을 적용하여 센서 좌표계 상에서의 자세를 결정하고 마지막으로 이로부터 위성의 실시간 위치 정보를 추정할 수 있다.
3. 별 추적기 모의 화면 생성
별 추적기 모의 화면을 생성하기 위해 별 카탈로그는 겉보기 등급 9등성 이상의 약 8만여 개의 별로 이루어진 HYG(Hipparcos Catalog, Yale Bright Star Catalog, Gliese Catalog of Nearby Stars)를 적용하였다. Table 1은 임계 겉보기 등급 이상의 별이 카탈로그에서 차지 하는 비율을 나타낸 것으로 HYG 카탈로그에서 겉보기 등급 8.0–9.0등급에 해당하는 별 개수가 50%만큼 차지하는 것을 알 수 있다. 일반적으로 별 추적기는 겉보기 등급 5.0–6.0 등급 이상의 별에 대한 영상을 확보하기 때문에 본 논문에서는 겉보기 등급 5.5 이상의 별 카탈로그에 대한 데이터베이스를 구축하였다.
| Apparent magnitude | 1.5 | 3.5 | 5.0 | 5.5 | 6.0 | 7.0 | 8.0 |
|---|---|---|---|---|---|---|---|
| Catalog occupancy percentage (%) | 0.029 | 0.350 | 1.969 | 3.447 | 6.097 | 15.832 | 23.676 |
Fig. 2는 별 추적기 CCD 카메라로 획득한 모의 화면 영상에 대하여 그레이스케일로 전환한 것을 도시한 것이다. Fig. 3과 같이 픽셀 값이 임계치 이상인 경우 해당 픽셀 값을 유지하고, 임계치 미만인 경우에는 픽셀 값을 그레이스케일 영상의 최저치인 0으로 이진화 과정을 거쳐 노이즈의 증폭을 방지함으로써 가우시안 필터에서 제거될 수 있게 하였다.

Fig. 4는 Fig. 3의 임계치에 따른 이진화 과정에 대한 상세 내용으로 좌측에 비해 우측이 임계치 처리 과정을 거쳤기 때문에 픽셀 위치에 따라 밝기가 다른 부분이 존재한다.
임계치에 따른 이진화 작업으로부터 산출한 픽셀 영역에 대해 중심점 찾기 알고리즘을 적용하기 전에 픽셀을 그룹화 하기 위해 가우시안 필터를 적용하였다[2]. 가우시안 필터링은 블러링 효과를 주어 픽셀의 깨짐을 보완한다. 실제 영상에서는 2차원 가우시안 분포 함수를 사용하는데, x와 y양축에 대해 정규분포가 독립성을 갖는다는 가정 하에 식 (1)과 같이 1차원 가우시안 분포 함수로 분리시켜 합성곱 할 수 있다. 1차원 가우시안 분포 함수는 식 (2)의 표준 정규분포를 이용한다. 여기서 σ는 표준편차를 의미한다.
가우시안 필터 적용을 통해 블러링한 영역을 한 레이블로 간주하고, 이들의 중심점을 찾기 위해 무게중심 알고리즘을 적용하였다. 무게중심 알고리즘은 픽셀 값에 가중치를 부여하여 픽셀 중심점 위치를 산출하는 원리로, 식 (3)과 같이 계산할 수 있다. 여기에서 A는 집합을 이루는 원소들의 픽셀 값(I[i,j])의 합이고, x̅와 y̅는 식 (4)에서 무게중심 알고리즘 기법으로 산출한 픽셀의 위치가 된다.
4. 별 인식 및 자세결정 알고리즘
위성의 자율항법을 위한 위치 추정을 위해 별센서가 별을 정확히 인식하여 자세 정보를 산출하는 것이 중요하다[3–7]. 별 추적기로 관측하여 확보한 별 영상과 카탈로그 기반의 데이터베이스를 비교하여 일치성을 파악하여 산출한다. 별 인식 알고리즘으로는 크게 삼각패턴, 그리드 알고리즘이 있다. 먼저, 삼각패턴 알고리즘은 별 추적기로 획득한 영상에서 3개의 별을 이용하여 삼각공식으로부터 패턴을 파악하는 원리를 가지며, 가장 밝은 별과 나머지 별에 대한 각거리를 구해 간단하지만 중심점 오차에 의해 인식 실패 확률이 커진다. 이에 비해 그리드 알고리즘을 적용하여 별을 인식하면 실제 별의 카탈로그 상에서 정의한 데이터베이스와 패턴을 비교하기 때문에 인식 정확도가 높다. 연산 속도가 느리다는 단점이 있지만, 중심점 오차가 존재하더라고 동일 그리드에 속하면 같은 별로 인식하게 되므로 정확도가 증가한다.
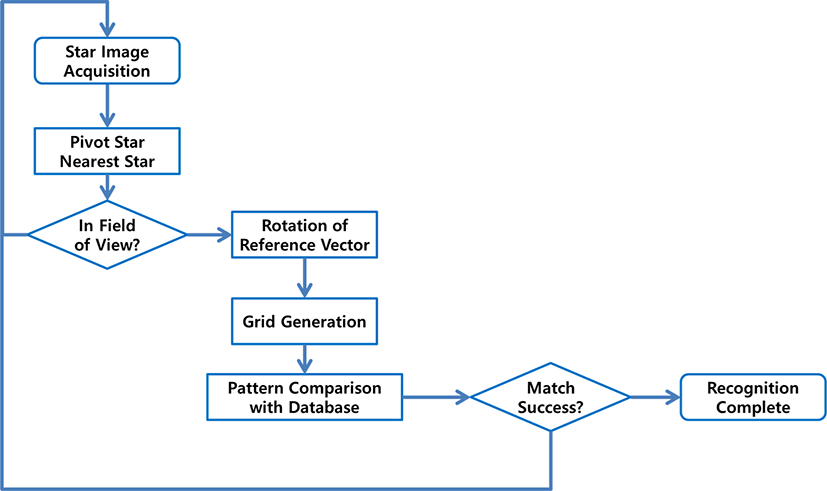
이러한 이유로 본 연구에서는 그리드 알고리즘으로부터 별 인식 알고리즘을 구현하였다. 그리드 알고리즘의 흐름도는 Fig. 5에 나타낸 바와 같다.
별 추적기로부터 획득한 영상에서 화면 중심에 가장 근접한 별을 Pivot star로 정의하고, 이와 가장 가까운 별을 nearest star로 정의하였다. 둘 간의 벡터를 기준으로 이미지 전체를 회전하고, 격자를 일정 간격으로 만들어 좌측 하단부터 번호를 매긴다. 이를 카탈로그로부터 생성한 데이터베이스와 순차 비교하여 별 인덱스를 찾아 인식하였다.
인식한 별을 이용하여 위성의 ECI 좌표계에서의 자세를 결정하는 알고리즘으로는 TRIAD 알고리즘을 적용하였다. TRIAD 알고리즘의 원리는 Fig. 6에서 동체 좌표계로 정의된 별 추적기 CCD 화면과 ECI 좌표계로 정의된 카탈로그 좌표계에서 별 벡터 간의 방향코사인 행렬을 구하는 것으로, 식 (5)와 같다. 여기서 방향코사인 행렬 A는 n개의 별에 대해 ECI 좌표계에 대한 별 시선벡터 와 동체 좌표계에 대한 시선 벡터 간의 관계식으로 정의된다.
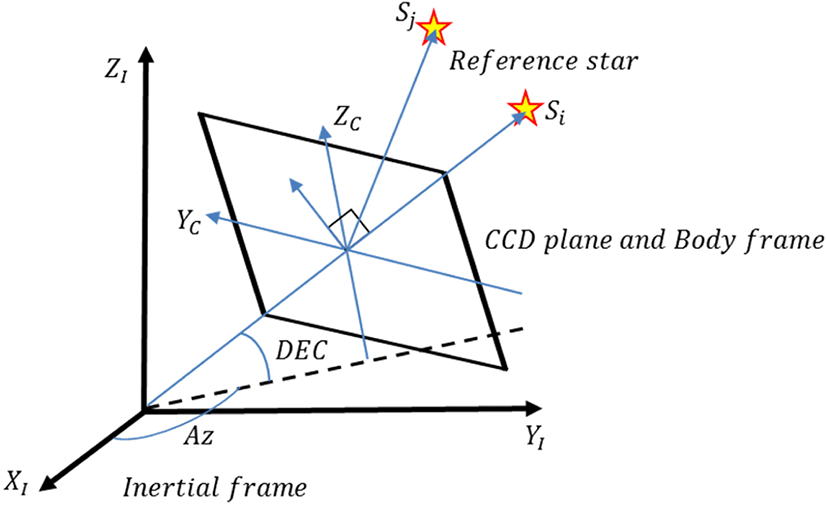
Fig. 7과 같이 2차원의 CCD 화면에 맺히는 정보는 실제 천구상의 별과 광축이 지나는 직선상에서 (U,V)로 표현할 수 있다. 여기에서 l은 별 추적기 시선 벡터가 CCD 화면 x축과 이루는 각도이고, λ는 CCD 화면 y축이 이루는 각도로써 초점거리를 활용하여 산출 가능하다.
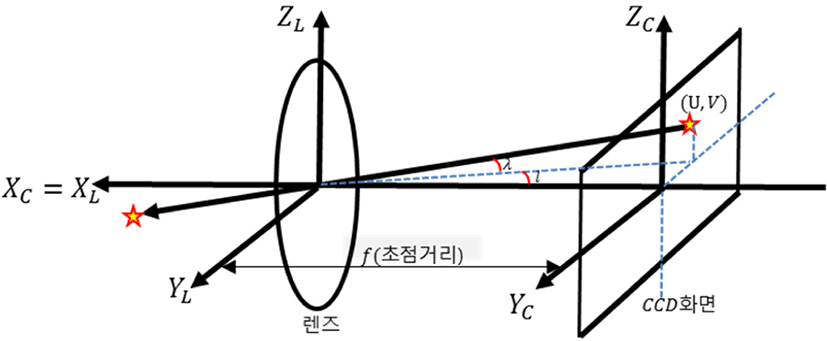
Fig. 6의 기하에 따라 식 (6)과 같이 를 산출할 수 있다. 또한 Fig. 7의 기하에 따라 식 (7)로부터 를 식 (8)처럼 산출할 수 있다. Az는 방위각, DEC는 고각 성분을 의미한다.
식 (5)에서 정의한 방향코사인 행렬 A는 관측된 3개의 별을 이용하여 식 (9)와 같이 산출 가능하다.
여기에서 위성의 자세 정보인 롤(ϕ), 피치(θ), 요(ψ)를 산출하기 위해 식 (10)의 방향코사인 행렬을 정의할 수 있다. 이때, 자세 정보 각각의 구속조건은 식 (11)에 기술한 바와 같다.
5. 인공위성 위치 추정 알고리즘
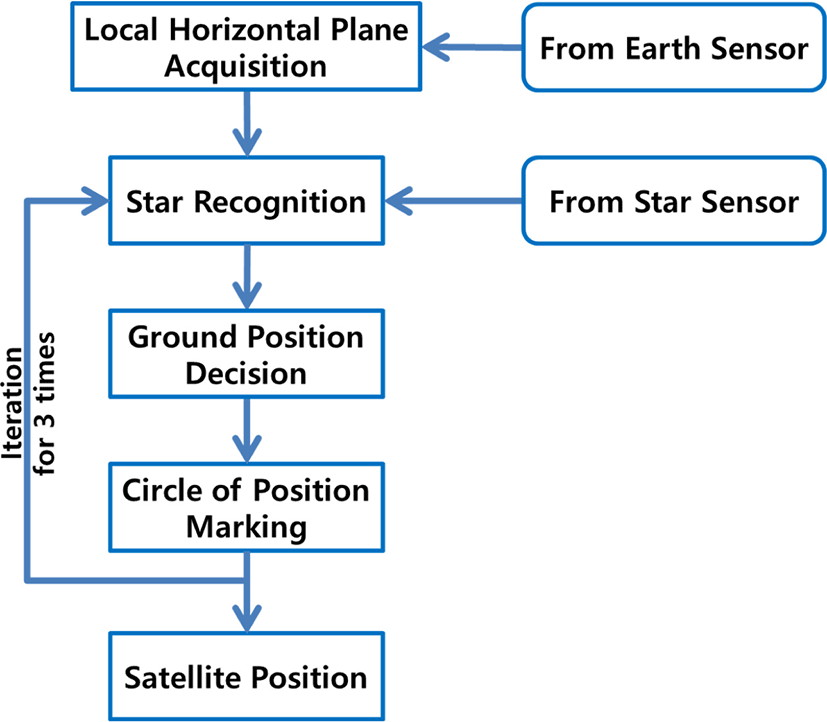
본 논문에서는 별 추적기로 획득한 위성의 ECI 좌표계 상에서의 자세 정보와 지구센서로부터 기 획득한 고도 정보를 이용하여 위성의 위치를 실시간 추정할 수 있음을 제안한다. 단, 지구센서로부터 획득하는 고도 정보는 위성의 동역학 방정식을 이용하여 산출 가능하도록 구성하였다[8]. Fig. 8은 위성의 위치를 결정하는 원리를 흐름도로 도시한 것이다. 별 추적기 2기로부터 위성의 관측각 정보를 산출하고, 이로부터 GP(ground position)을 결정할 수 있다. 2개의 GP로부터 위성의 위치는 국부 수평면 상에서 원의 교점 2개로 귀결된다. Fig. 9는 국부 수평면에서의 별의 관측각 정보를 산출하는 원리를 나타낸다. 천정(zenith)으로부터 위성의 별 관측각을 H라 하고, 식 (12)–(17)을 통해 위성의 위치를 추정할 수 있다. 이때, h는 위성의 지표면으로부터 고도 정보로써 위성의 동역학 모델로부터 산출하였다. rd는 지구 중심으로부터 가상의 별까지의 거리이고, ρr은 위성부터 가상의 별까지의 거리이다.
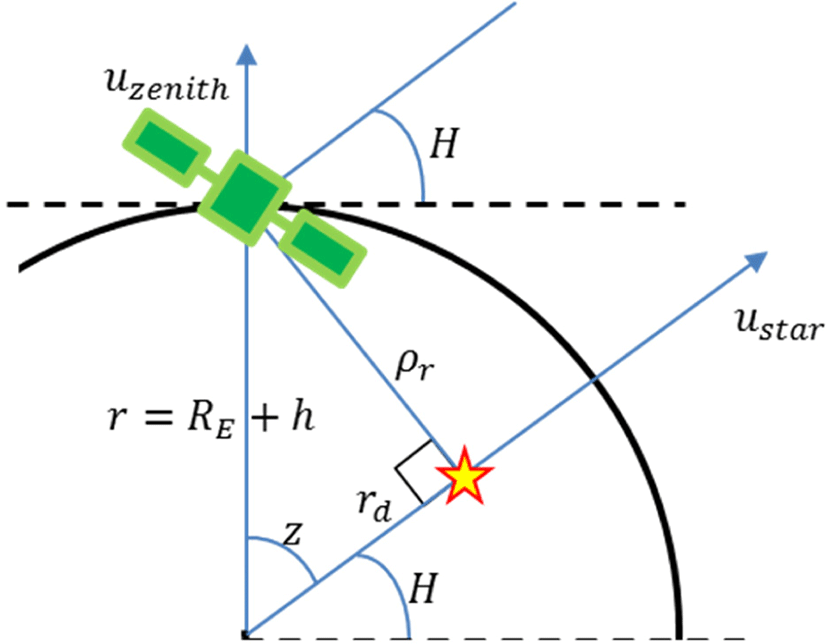
별 추적기 2기에 대한 정보를 이용하여 교점을 산출하기 때문에 식 (16)과 같이 위성의 위치 (XI,YI,ZI)와 가상 별 위치(x1,y1,z1),(x2,y2,z2) 간의 기하관계를 활용하면, 식 (17)과 같이 방정식을 풀이할 수 있다.
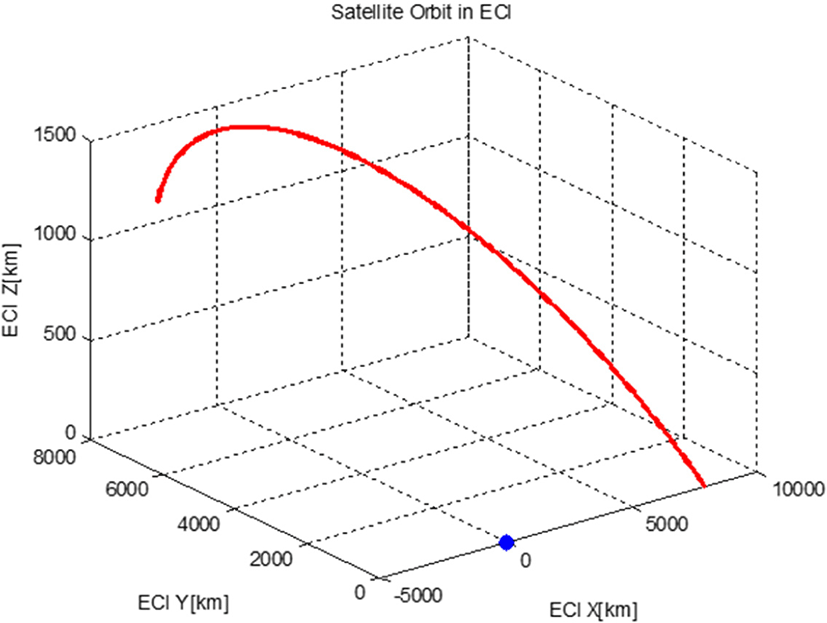
이러한 위치 추정 알고리즘 검증을 위하여 사용한 주기 4,800초의 3자유도 위성 동역학으로부터 계산한 위성의 ECI 좌표계에서의 위치 정보는 Fig. 10에 도시한 바와 같다. 이때의 ECI 좌표계 상에서의 위성 자세, 위치 추정 오차는 Tables 2와 3에 기술하였다. 위성 자세 오차 평균이 피치각 0.0153도, 요 0.0224도가 발생하는 이유는 별 영상 처리 시 중심점을 찾을 때 빛 번짐, 중심별의 뭉침 현상 때문이다. 특히 롤 각 오차 평균이 0.0458도로 2배 이상 크게 발생하는 이유는 별 추적기 카메라가 기울어짐에 따라 영상의 별 이미지가 화면 중심 방향으로 회전하기 때문이다. 위성 위치 추정은 자세 추정 오차가 반영된 결과로써, 고도 방향으로 516.2 m의 오차 평균이 발생한 것을 확인할 수 있었다.
| Roll | Pitch | Yaw | |
|---|---|---|---|
| Error mean value | 0.0458 | 0.0153 | 0.0224 |
| Error standard deviation | 0.0210 | 0.0302 | 0.008 |
| x | y | z | |
|---|---|---|---|
| Error mean value | 325.1 | 265.7 | 516.2 |
| Error standard deviation | 27.73 | 18.19 | 14.43 |
6. 결론
일반적으로 위성의 위치 추정을 위해 GPS를 이용한 반능동적 방식의 항법이 사용되지만, 통신 두절과 송, 수신 시계에 따른 항법 오차가 발생하게 된다. 이러한 오차 발생은 위성의 실시간 위치 추정을 어렵게 하여, 자율항법이 이루어질 수 없다.
따라서 본 논문에서는 별센서를 이용한 위성 자세 정보를 추정하고, 위성 동역학 방정식으로부터 위성의 고도 정보를 획득 및 활용하여 위성의 실시간 위치 계산을 할 수 있는 기법을 제시하였으며 검증을 위해 별 추적기 시뮬레이터를 구성하였다. 별 추적기 시뮬레이터는 별 추적기 2대로 구성되어 획득한 천구 영상으로부터 영상처리를 통해 별 인식을 완료하고, 이로부터 위성의 ECI 좌표계에서의 자세 및 위치를 추정한다. 별 인식을 위한 알고리즘으로는 그리드 알고리즘을 이용하여 영상의 패턴을 확보하였다. 인식한 별로부터 TRIAD 알고리즘을 적용하여 위성의 ECI 좌표계에서의 자세를 산출하고, 고도 정보가 주어질 때 위치를 추정할 수 있다.
지구 저궤도뿐만 아니라 심우주에서의 위성 자율항법 수행을 위해서는 지상에서 충분한 검증이 이루어져야 하고, 본 논문에서 제시한 별 추적기 알고리즘을 기반으로 항법 성능 분석 및 위치 추정 정확도 향상 연구에 활용할 수 있을 것으로 기대된다.