Journal of Space Technology and Applications

The Korean Space Science Society

J. Space Technol. Appl. 2025; 5(1):47-60

pISSN: 2765-7469

DOI: https://doi.org/10.52912/jsta.2025.5.1.47

기술논문

엔지니어링 최적 설계 및 적용: 다중 위성 및 지상안테나의 영상 임무운영 스케줄링 관점에서

이정현¹^,^†

Engineering Optimal Design and Application: In Terms of Imaging Mission Scheduling for Multiple Satellites and Ground Antennas

Junghyun Lee¹^,^†

¹한국항공우주연구원

¹Korea Aerospace Research Institute, Daejeon 34133, Korea

^†Corresponding author : Junghyun Lee, Tel : +82-42-870-3946, E-mail : jhlee16@kari.re.kr

© Copyright 2025 The Korean Space Science Society. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Jan 12, 2025; Revised: Jan 29, 2025; Accepted: Feb 01, 2025

Published Online: Feb 28, 2025

요 약

This technical report discusses optimization and optimal design methodologies in engineering. Optimization modeling is that converting physical phenomenon to an objective function within constraints and expressing optimization equation. The objective function depends on design variables, which must be determined based on optimal cost and utility. Then, optimal solutions can be derived using deterministic or stochastic approaches. Deterministic approaches guarantee global optimum using convexity and Karush-Kuhn-Tucker conditions, whereas stochastic approaches employ probabilistic techniques to approach global optimum. These approaches are complementary, selected based on the problem characteristics. Deterministic approaches ensure solutions applying continuous, independent variables; which lead to exponential computational complexity with increased variables. While, stochastic approaches using random functions and statistical techniques, handle nonlinear and discrete problems but cannot guarantee global optimum. A case study introduces imaging mission operation of multiple satellites. It applies a deterministic mixed-integer linear programming (MILP) approach and a stochastic genetic algorithm (GA). GA offers flexibility in nonlinear models and discrete spaces, making it suitable for complex problems to find near-optimal solutions. MILP limited to linear models but ensures global optimum. Simulation results show GA's applicability and utility in diverse operational modes and complex missions, while MILP excels in maximizing resource utilization and finding optimal solutions within design constraints. This study demonstrates the potential of optimization techniques for efficient multi-satellite operations and suggests expanding to more complex systems.

Abstract

공학에서의 최적화 및 최적 설계 방법론에 대해 논의한다. 최적화 모델링은 실제 물리적 현상을 제약 조건 내에서 목적 함수를 정의하고 최적화 식으로 표현하는 것을 말한다. 목적함수는 엔지니어가 설계하는 변수에 따라 구성이 되는데 최적의 비용과 효용에 따라 설계 변수는 결정되어야 한다. 최적화 모델링 이후에 최적해를 도출하여야 하는데, 결정론적 방법과 추계적 접근법이 있다. 결정론적 접근법은 볼록성과 Karush-Kuhn-Tucker 조건을 활용하여 전역 최적해를 보장하는 반면, 추계적 접근법은 확률적 기법을 사용하여 전역 최적해에 접근한다. 이 두 접근법은 상호 보완적 특성을 가지며 문제의 특성에 따라 선택적으로 적용된다. 결정론적 방법은 연속적이고 독립적인 변수를 기반으로 해를 보장하지만, 변수의 증가에 따라 계산 복잡도가 기하급수적으로 증가하는 단점이 있다. 반면, 추계적 방법은 랜덤 함수 및 통계적 기법을 활용하여 비선형 및 비연속적 문제에 적용 가능하며 전역 최적해를 보여(show) 줄 수는 있지만 보장(guarantee)하지 못한다는 한계를 가진다. 사례 연구를 위해 다중위성에서의 영상임무운영 최적화 연구 사례를 소개한다. 혼합정수선형계획법을 이용한 결정론적 방법과 유전 알고리즘을 활용한 추계적 접근법을 나타내었다. 유전 알고리즘은 비선형 모델과 이산 공간에서 높은 유연성을 제공하며, 복잡한 문제에서도 준최적해를 탐색하는 데 적합하다. 반면, 혼합정수선형계획법는 선형 모델로 제한되지만, 전역 최적해를 보장하는 특성을 가진다. 시뮬레이션 결과, 유전 알고리즘은 다양한 운영 모드, 복잡한 모델링, 및 영상 임무에서 적용 가능성 및 효용성을 가졌으며, 혼합정수선형계획법은 적용은 제한적이나 자원 활용도를 극대화하면서 설계 범위 내에서 최적해를 도출하는 데 우수한 성능을 보였다. 결론적으로, 본 연구는 다중 위성의 효율적 운영을 위한 최적화 기술의 잠재력을 입증하며, 향후 더 복잡한 시스템으로의 확장을 제안한다.

Keywords: 최적 설계; 모델링 및 시뮬레이션; 결정론적 및 추계적 접근; 다중위성의 영상임무 운영

Keywords: engineering optimal design; modeling and simulation; deterministic and stochastic approaches; imaging mission operation of multiple satellites

1. 최적화 모델링

전통적인 공학에서 모델링은 물리와 수학을 기반으로 실제 현상을 유한한 입력(input)과 출력(output)을 가지는 함수 및 수학적인 형태로 표현하는 과정을 의미하며 이러한 함수 및 수식을 푸는 과정을 시뮬레이션으로 정의할 수 있다[1,2]. 컴퓨터를 활용하여 GUI(graphical user interface) 를 통해 설계 결과를 시각화하고, 애니메이션으로 결과를 보여주는 작업을 모델링 및 시뮬레이션이라고 생각하기 쉽다. 물론 이것도 모델링 및 시뮬레이션의 한 형태이다. 다만, 이러한 접근은 수학 및 물리 모델을 기반으로 한 작업을 GUI를 통해 가시적으로 표현한 것일 뿐이다. 대부분의 경우, 문제를 분석적으로(analytic) 바로 해결할 수 없으므로 수치해석(numerical analysis)의 도움을 받아야 한다. 시간 변화 시스템(time-variant system)을 해석하는 경우, 수치해석에서 증분(increment)은 단위 시간으로 정의되며, 이 경우 애니메이션으로 표현할 수 있다. 대표적인 예로 유한요소법(finite element method, FEM), 전산유체역학(computational fluid dynamics, CFD), Simulink 등이 있다[3,4]. 또한, 전공 서적에서 다루는 문제 역시 모델링 및 시뮬레이션의 한 사례로 볼 수 있다. 물리적 현상을 수식으로 표현한 것이 모델링이며, 이를 수작업으로 풀이하더라도 훌륭한 시뮬레이션 결과를 도출할 수 있다. 수치해석, 분석적 접근, GUI, 수학 등은 그 자체로써 의미를 갖기보다는 모델링 및 시뮬레이션을 위한 하나의 도구이다.

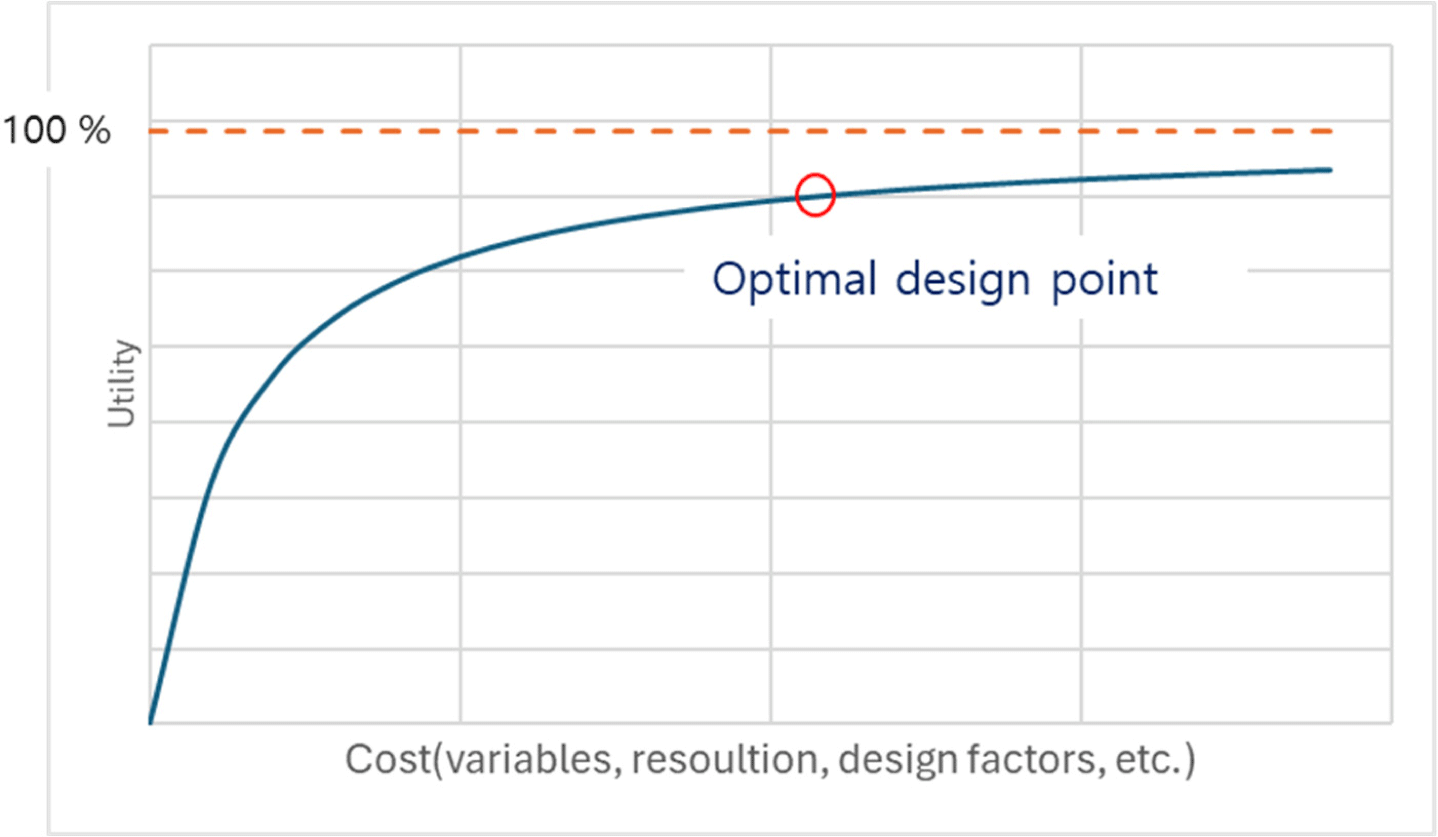
이제 개념을 좀 더 확장해 보자. 공학적 관점에서의 최적화 및 최적 설계는 두 단계로 나눌 수 있다. 첫 번째 단계는 현재 문제를 제약조건과 절차를 고려하여 최적화 공식으로 표현하는 것이다. 이는 설계 및 모델링과 밀접한 연관이 있다. 공학적 현상에 영향을 미치는 변수는 무수히 많으며, 하나의 변수에서 여러 가지 공학적 의미를 가진 현상이 나타날 수 있다. 공학적 현상 및 변수들 간에는 상호 상관 관계(correlation)가 존재한다. 가능한 많은 변수와 현상을 고려하는 것이 정확성을 높이는 데 도움이 되지만, 높은 정밀도를 요구할수록 계산 비용은 기하급수적으로 증가한다. 자연과학과 공학의 가장 큰 차이는 공학에서는 비용(cost)와 효용(utility)를 고려한다는 점이다. 최적 지점을 결정하는 것이 하나의 중요한 모델링이다(Fig. 1). 실제 문제를 최적화 식으로 정의했다는 것 자체가 큰 의미를 가진다. 이는 해당 문제를 최적화 알고리즘을 통해 풀이할 수 있음을 의미하기 때문이다.

Fig. 1. Optimum design point considering cost and utility.

Download Original Figure

해석하고자 하는 공학적 현상을 목적 함수(objective function)로 정의해야 하며, 이에 영향을 미치는 변수들 중 주요 변수는 엔지니어에 의해 설계 변수(design variable)로 선택된다. 최소한의 설계 변수로 설계 허용 범위 내에서 문제를 정의해야 한다. 설계 변수와 해석 대상 현상 간의 관계는 최적화의 목적 함수로 표현된다. 설계 변수는 서로 독립적인 것이 이상적이며, 만약 상호 상관 관계가 존재하면 변수 조정 시 최적화가 어려워질 수 있다. 다변수 최적화 공식은 일반적으로 식 (1)과 같이 표현된다[5].

■ General optimization formulization − Objective function • Min f (X ¯) − Design variable • X ¯ = (x 1, x 2, x 3, ⋯ .) − Constraint • g (X ¯) i ≤ 0, i = 1 to p • h (X ¯) j = 0, j = 1 to m

(1)

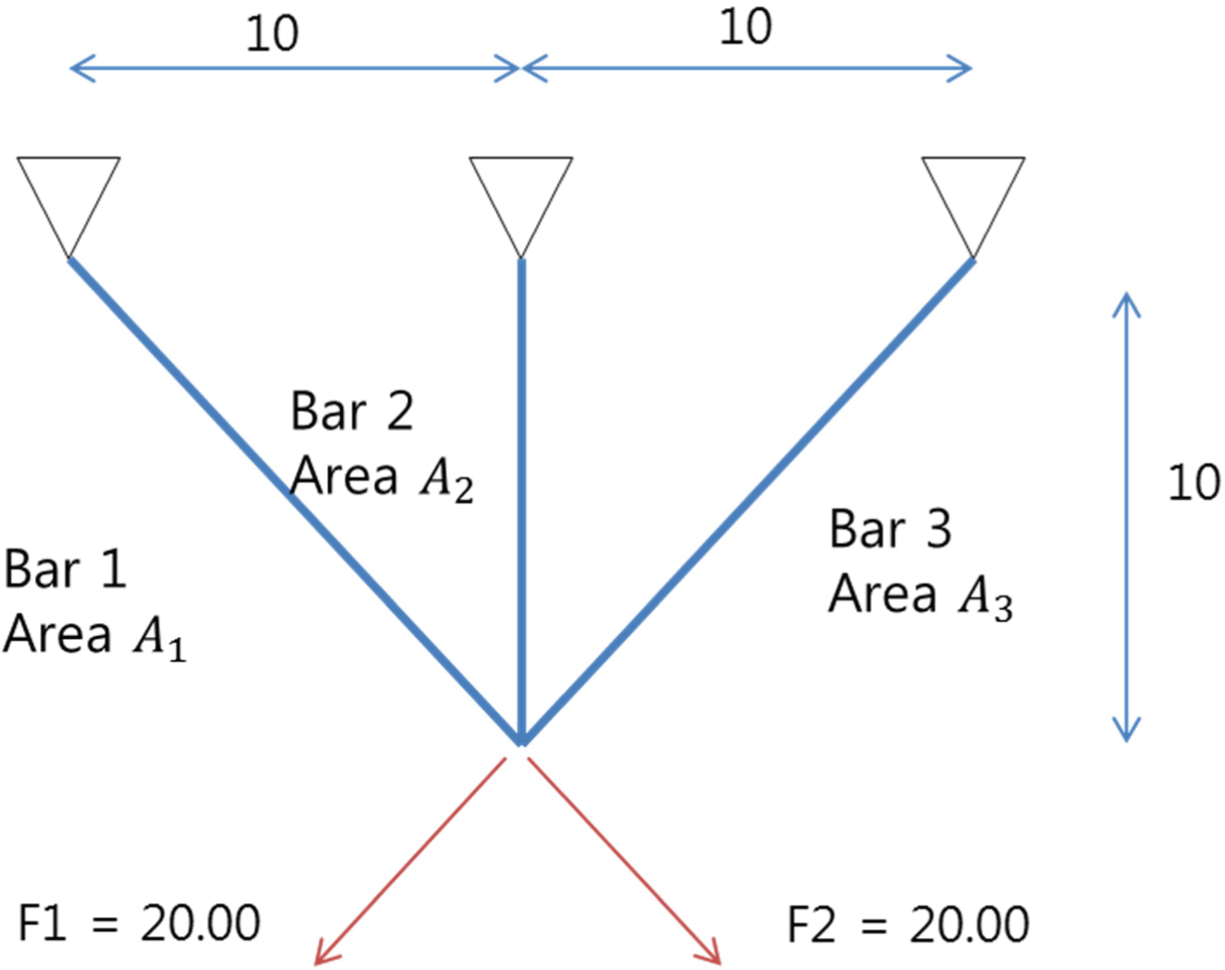
다음 단계로는 공식이 세워진 이후에 주어진 제약 조건 내에서 최대 혹은 최소의 목적값을 찾는 것이다. 최적화 문제를 해결하는 라이브러리는 많이 개발 및 공개가 되어 있다. 구조 최적화 혹은 전기 시스템 최적화에서 일반적으로 변수들이 상호 직교(orthogonal)하며 변수들은 연속(continuous)이거나 구간 연속(piecewise continuous) 하며, 이 경우에는 라이브러리의 적용이 수월하다. 단순한 구조 최적설계의 예시는 Fig. 2 및 식 (2)와 같다 [6].

Fig. 2. Simple structure modeling [].

Download Original Figure

■ Structure optimization − Description • Minimize bar volume within allowable stress − Formulization • Minimize f (A) = 10 (22 A 1 + A 2) • Subject to 2 A 1 + 2 A 2 2 A 1 (A 1 + 2 A 2) < 1 1 A 1 + 2 A 2 < 1 • Bounded to 0.1 < A 1 < 100, 0.1 < A 2 < 100

(2)

2. 추계적 및 결정론적 접근법

최적 설계에 대한 접근법은 크게 결정론적(deterministic)과 추계적(stochastic)으로 구분된다. 이 두 접근법은 상호 보완성을 가지며 적용 문제의 특성에 따라 적절히 선택된다. 결정론적 접근법은 일반적으로 미분 혹은 물리적 민감도(sensitivity)를 활용하여 최적해를 도출한다. 변수의 증가에 따라 차원의 저주(curse of dimensionality)가 발생하며[7], 지역 최적해(local optimum)에 수렴하는 경향이 있다. 그러나 주어진 시행 및 허용 오차(tolerance) 내에서 해를 보장할 수 있는 장점이 있다. 결정론적 접근법은 매 시행에서 동일한 결과를 도출한다는 특징을 가지며, 변수들이 독립적이고 연속적일 때 적용 가능하다. 주요 기법으로는 Newton-Raphson method, Quasi-Newton's methods, steepest descent method, adjoint method 등이 있다. 이러한 방법은 상대적으로 저차원의 문제에 적합하며, 전역 최적해(global optimum)에 접근하기 위해 추가적인 보완이 필요할 수 있다.

추계적 방법은 랜덤 함수와 통계적 기법 등을 활용하여 복잡한 비선형 및 비연속적 문제를 해결한다. 이 방법은 전역 최적해에 접근하지만 보장하지 못한다는 한계를 가진다. 복잡한 상태 공간에서는 명확히 예측하기 어려운 경우가 많다. 추계적 방법으로 도출된 해는 수학적으로 엄밀히 증명되기보다는, 그래프 등의 시각적 표현을 통해 검증되는 경우가 일반적이다. 주요 기법으로는 simulated annealing, genetic algorithm, particle swarm optimization, ant colony optimization, random search 등이 있다. 추계적 방법은 매 시행에서 다른 결과를 도출하며, 특히 전역 최적화(global optimization)에 유리한 특성을 가진다[8,9].

결정론적 방법과 추계적 방법 간의 쌍대성은 Table 1에 요약되어 있다. 완전히 분리된 개념으로 보기는 어렵지만 일반적으로 두 접근법은 Table 1과 같은 특성을 가진다.

Table 1. Trends according to deterministic stochastic approach

	Deterministic	Stochastic
Solution	Local optimum approach	Global optimum approach
Algorithm cost as variable increase	Course of dimension	High cost at initial condition increase linearly
Variable condition	Orthogonal, continuous or piecewise continuous	Undefined
Application	Low complexity problem	High complexity problem
Derived solution	Guaranteed within given tolerance	not guaranteed
Iteration	Defined	Undefined

Download Excel Table

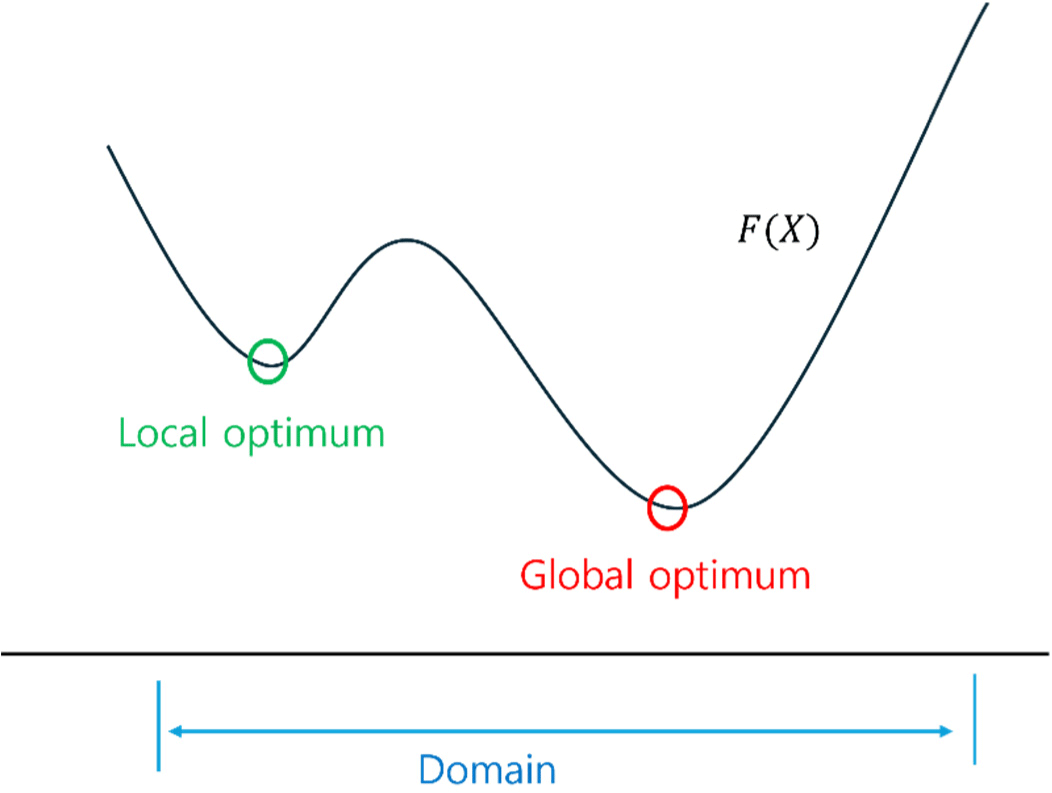
상태 공간은 주변부에 비해 최소점인 지역 최적화와 상태공간 전체에 대한 최소점인 전역최적화가 있다(Fig. 3). 최적화의 궁극적인 목표는 상태 공간에서 전역 최적해를 찾는 것이다. 그러나 초기 해가 지역 최적해 근처에 위치하는 경우, 조기 수렴(premature convergence)으로 인해 전역 최적해 탐색에 실패할 가능성이 높다. Fig. 3과 같이 단순한 문제의 경우에는 직관적으로는 상태 공간에서 지역 및 전역 최적해의 위치를 시각적으로 식별할 수 있지만, 고차원의 설계 공간 및 복잡한 변수 관계가 있는 문제에서는 이를 명확히 표현하기 어렵다. 따라서, 전역 최적해를 탐색하기 위한 효율적인 알고리즘의 개발 및 도출된 해의 검증(validation) 과정이 필수적이다.

Fig. 3. Global and local optimum.

Download Original Figure

3. 전역최적해 도출

3.1 볼록 최적화 및 결정론적 접근

공학적으로 이상적인 최적 설계는 물리적 모델을 볼록성(convexity)가 보장되는 최적화 수식으로 변환하고, 카루지-쿤-터커(Karush-Kuhn-Tucker, KKT) 조건을 만족함으로써 전역 최적해를 도출하는 것이다. 도출된 전역 최적해는 주어진 수치적 허용 오차(tolerance) 내에서 검증(validate)될 수 있다.

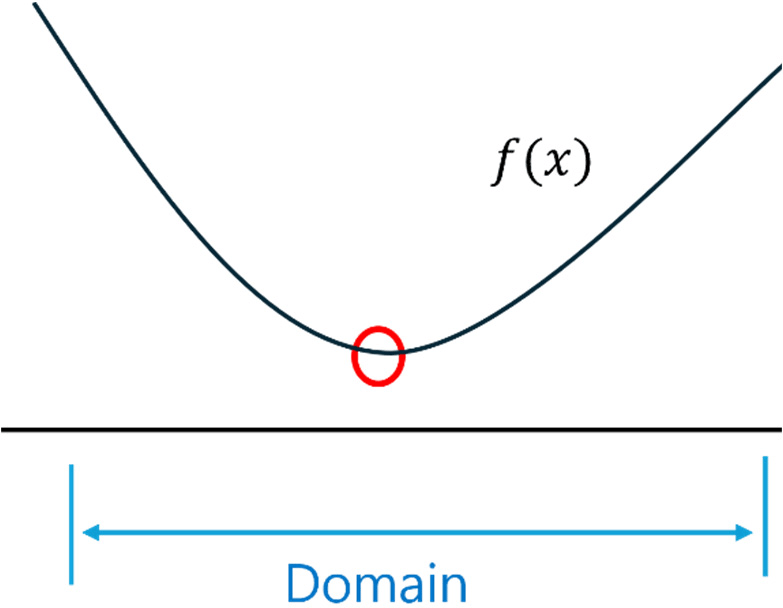
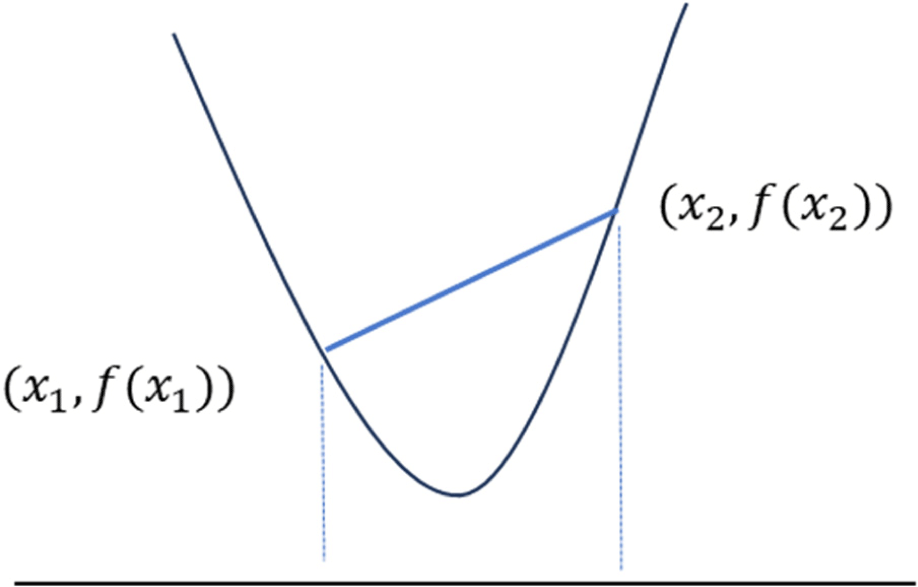
단일 변수의 전역 최적해는 식 (3) 및 Fig. 4와 같이 정의할 수 있다. 함수의 이차 도함수는 곡선의 곡률(curvature)을 나타내며, 정의역(domain) 내에서 이 값이 양수라면 해당 함수는 볼록성을 보장한다. 이때, 일차 도함수가 0이 되는 지점은 전역 최적해(global optimum)가 된다.

Fig. 4. Global optimality in case of one variable.

Download Original Figure

■ One variable case, y = f (x) : Domain is closed and bounded • f ¨ (x) > 0 within given domain • Satisfying f ˙ (x *) = 0, x * is global minimum

(3)

단일 변수 함수를 통해 복잡한 다변수로 구성된 최적화 모델에 대한 전역 최적해 접근에 대해서 직관적으로 이해할 수 있다. 단일 변수에 대해서와 마찬가지로 주어진 정의역에서의 볼록성을 만족시킬 때 미분값이 전역 최적해이다. 식 (4) 및 Fig. 5와 같이 목적함수 f(X)와 제약조건의 볼록성을 보장해야 한다. 목적함수에 대해서 정의역이 볼록 집합(convex set)이라고 가정 시 정의역 내에 임의의 2개의 값에 대한 목적함수의 출력값을 선형보간으로 연결했을 때에 그 범위 내에서 목적함수 값은 선형보간으로 연결한 값보다 항상 작다. 목적함수에 대해서는 이러한 볼록성을 보장해야 하며, 수학적으로 목적함수의 헤시안(Hessian)에 대해 양의 정부호(positive definite)인 경우에 목적함수의 볼록성이 보장된다. 제약조건에 대해서도 비선형 제약(inequality constraints)은 볼록성, 선형 제약(equality constraints)는 아핀(affine)을 각각 만족하여야 한다[10].

Fig. 5. Convexity in convex set.

Download Original Figure

■ Convexity of the objective function − 목적함수 f (X ¯) 에 대해 f (α x 1 + (1 − α) x 2) ≤ α f (x 1) + (1 − α) f (x 2), ∀ x 1, x 2 ∈ domain of f, α ∈ [0, 1] − 제약 조건 g j (x) ≤ 0 은 convex, h i (x) = 0 이 affine

(4)

다음으로는 식 (5)와 같이 KKT 조건을 만족하여야 한다. 식 (1) 에 라그랑지안 승수(Lagrangian multiplier)를 이용하면 라그랑지안 함수(Lagrangian function)으로 표현 가능하다. 단일 변수의 예시와 같이 1차 및 2차 미분값에 대해 민감도가 없는 후보군을 도출 할 수 있다.

■ Satisfying KKT conditions L (X ¯, v, u, s) = f (X ¯) + ∑ i = 1 p v i h i (x) + ∑ j = 1 m u j g j (x) − 1 st order necessary condition • Gradient condition ■ ∂ L ∂ x k = ∂ f ∂ x k + ∑ i = 1 p v i ∂ h i ∂ x k + ∑ j = 1 m u j ∂ g j ∂ x k = 0 • Feasibility condition ■ h i (x) = 0; g j (x) ≤ 0; • Switching condition ■ u j g j (x) = 0; • Non-negative of lagrange multipliers for inequalities . u j ≥ 0 − 2 st order Necessary condition • ∇ 2 L = ∇ 2 f + ∑ i = 1 p v i ∇ 2 h i + ∑ j = 1 m u j ∇ 2 g j (x) • Let there be nonzero feasible directions, d ≠ 0, ■ Q ≥ 0, where, Q = d T ∇ 2 L (x) d

(5)

도출된 해가 볼록성과 KKT 조건을 모두 만족하면 전역최적이다. 단순한 모델의 경우에는 해석적(analytic)으로 풀 수 있고 필요한 경우에 미분 혹은 민감도 기반 결정론적 접근법을 사용할 수 있다. 도출된 값은 주어진 수치적 공자 안에서 전역최적을 보증하게 된다.

3.2 추계적 접근법

추계적 접근법은 결정론적 접근법의 여집합 개념이다. 상태공간의 볼록성이 입증되기 어려운 경우, 이산 공간(discrete space)처럼 변수 간의 직교성 및 연속성 등이 보장되지 않은 경우에 전역 최적해의 접근을 위해 추계적 접근법을 사용한다. 그리고, NP-hand 문제처럼 특정 알고리즘으로 문제를 해결하지 못하며, 모든 경우에 대입해야 문제를 풀 수 있는 경우에 사용한다. 전역최적해의 탐색을 위해서는 조기 수렴해(premature solution)으로 빠지지 않기 위한 알고리즘 설계를 필요로 한다. 대표적인 유전 알고리즘(genetic algorithm, GA)의 예를 들어서 기술하면, GA는 자연의 진화 과정을 모방하여 최적화를 수행하는 알고리즘으로 상태 공간에서 최적의 값을 찾는 데 사용된다. 설계 변수(design variable)를 염색체(chromosome)로 나타내며 적합도(fitness), 돌연변이(mutation)와 같은 개념을 도입하여 문제를 해결한다. 염색체는 상태 공간의 값을 표현하며, 적합도는 특정해가 문제에 얼마나 적합한지를 나타내는 척도이다. GA의 핵심은 진화를 통해 세대가 반복될수록 적합도 값이 점진적으로 향상된다는 점이다. GA에서는 세대가 진행됨에 따라 적합도가 갈수록 증가해야 되는데, 마찬가지로 조기 수렴해를 도출할 수 있다. 염색체를 설계할 때 상태공간 전체를 나타낼 수 있어야 한다. 충분한 수의 개체군(population)을 통해 상태공간 전체를 골고루 탐색할 수 있어야 한다. 그 뿐 아니라, 교차(crossover)시 적절하게 열성 인자들도 섞어서 탐색해야 하며 돌연변이 비율도 적절한 탐색의 필수적인 요소이다.

4. Case Study

저궤도 다중 위성 및 지상안테나의 영상 임무 운영 스케줄링 문제를 최적화하기 위한 추계적 및 결정론적 접근법의 차이를 소개하고 두 접근법의 성능과 활용 가능성을 비교한다. 기존에 진행되었던 연구에 대해 최적설계 접근 관점에서 비교 및 요약한 기술이다[11–13].

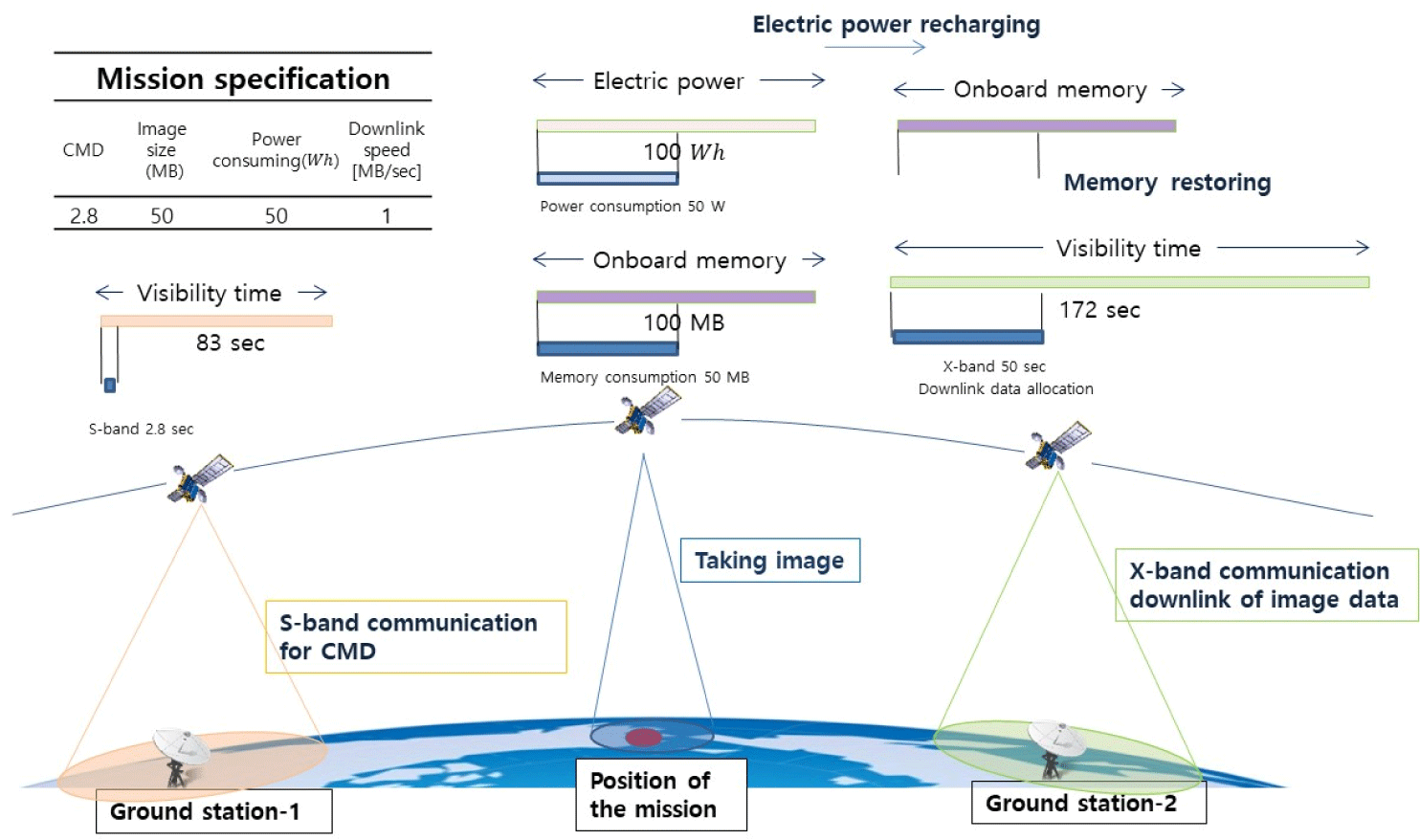
영상 촬영을 위한 명령은 S-band 안테나를 통해 지상에서 위성으로 전송이 된다. 위성은 수요기관의 촬영 요청에 따라 촬영 지점을 지날 때에 자세제어 등을 통해서 해당 지점을 지향함으로써 영상을 획득한다. 획득된 영상은 다음 지상 안테나와의 교신 시 지상으로 하향 전송된다. 이러한 일련의 절차는 작업을 자원에 할당하는 스케줄링 및 스케줄링 최적화로 표현 가능하다.

S-밴드를 통한 명령 전송, X-밴드를 통한 영상 하향 전송을 위한 시간은 위성과 지상 안테나 간의 통신 가시권에 할당된다. 또한, 영상 촬영 시 자세를 조정하는 과정에서 전력을 소모하며 촬영된 영상은 위성 내부의 온보드 메모리에 저장된다. 자원 이외의 제약조건도 가지고 있다. 첫째로는 다수의 위성과 다수의 지상 안테나간 가시권 충돌이 발생할 수 있다. 그리고 S-밴드를 통한 명령 상향 전송, 명령을 기반으로 한 영상 촬영 그리고 저장된 영상의 지상으로의 하향 전송은 동일한 위성에 대해 정해진 일련의 순서에 따라서 할당되어야 한다. 이러한 운영 과정에서 최적화의 목적은 제한된 자원을 효율적으로 사용하며 임무의 성과를 극대화하는 데 있다. Fig. 6과 아래에 관련된 내용이 도시화 되어 있다. 위성이 주어진 궤도에 따라 움직이며 영상 촬영 임무에 대한 Spec이 기술되어 있다. 처음에 촬영 명령 전송을 위해 S-밴드 가시권 시간 83초에 대해 2.8초를 할당하고 위성에서는 주어진 명령을 가지고 영상 지점을 지날 때에 50 W의 전력을 소모하여 촬영을 한다. 그리고 영상은 위성 내의 온보드 메모리에 50 MB만큼 할당이 된다. 다음 X-밴드 교신 때에 하향 링크 속도에 따라 X-밴드에 50초를 할당한다.

Fig. 6. Imaging mission operation sequence [].

Download Original Figure

목적함수: 영상촬영 데이터, 개수, 사용자 이익 등의 극대화 등
작업: 영상 임무 수행과 관련된 행위
자원: 통신 가시권, 전력, 메모리 등
제약조건: 가시권 충돌, 영상 촬영 시퀀스 등

위의 최적화 모델에 대해 추계적 및 결정론적 접근에 대한 연구를 소개 및 비교하고자 한다.

4.1 추계적 접근법 – 유전 알고리즘

다중 위성과 다수의 지상국 간의 이미지 획득 임무를 효율적으로 스케줄링하기 위해 GA를 활용한 최적화 기법이 제안되었다[11,12]. 이 접근법은 위성 자원(전력, 메모리) 및 통신 가시 성 충돌과 같은 현실적인 제약 조건을 통합적으로 고려하며 스케줄링 문제를 해결하는 데 목적을 두고 있다. 스케줄링 모델은 대한민국에서 운영 중인 국가 위성의 궤도를 참고하여 설계되었으며, 다중 위성의 가시권 충돌, 다중 위성과 지상국의 상호작용, 자원의 덤프와 복구 과정을 모두 포함하도록 정의되었다.

영상 임무 운영의 특성을 반영하여 본 연구는 스케줄링 문제를 명확히 모델링하였다. 위성은 명령 업링크, 영상 촬영, 영상 데이터 저장, 데이터 다운로드라는 작업 순서를 따라야 하며, 각 작업은 시간적 연계성과 자원 소비를 필수적으로 고려해야 한다. 이러한 모델을 기반으로 GA는 다중 목표를 최적화할 수 있는 도구로 설계되었다. 이 모델은 사용자 우선순위, 마감 기한, 이익, 구름 조건, 긴급 상황과 같은 요소를 통합하여 최적화 문제를 해결하며, 알고리즘은 각 임무에 대해 적합도를 평가하고, 교차 및 돌연변이 연산을 통해 점진적으로 더 나은 해를 탐색한다.

다목적실용위성 시리즈 위성의 데이터를 기반으로 더미 데이터를 생성하여 시뮬레이션을 수행하였다. 다섯 대의 위성과 세 개의 지상국으로 구성된 가상 시스템에서 다양한 임무 시나리오를 실험하였으며, 제안된 알고리즘의 실효성을 검증하였다. 시뮬레이션 결과, GA는 일반, 상업, 전술의 세 가지 운영 모드에서 모두 현실적인 제약 조건을 충족하면서 적합한 스케줄링을 생성하였다. 설계된 알고리즘은 최적 또는 근사 최적의 스케줄을 도출하며, 자원 사용의 효율성과 임무 수행 성공률을 크게 향상시키는 결과를 보였다.

50개의 임무에 대해 5개의 위성의 자윈(온보드 메모리 및 전력)에 스케줄링된 결과는 Fig. 7과 같다. 알고리즘 결과 도출에는 약 8시간이 소요되었으며 가시권을 포함한 상세 결과는 상기 논문에 자세히 나타나 있다[11, 12].

Fig. 7. The scheduling results of electric power and on-board memory consumption [].

Download Original Figure

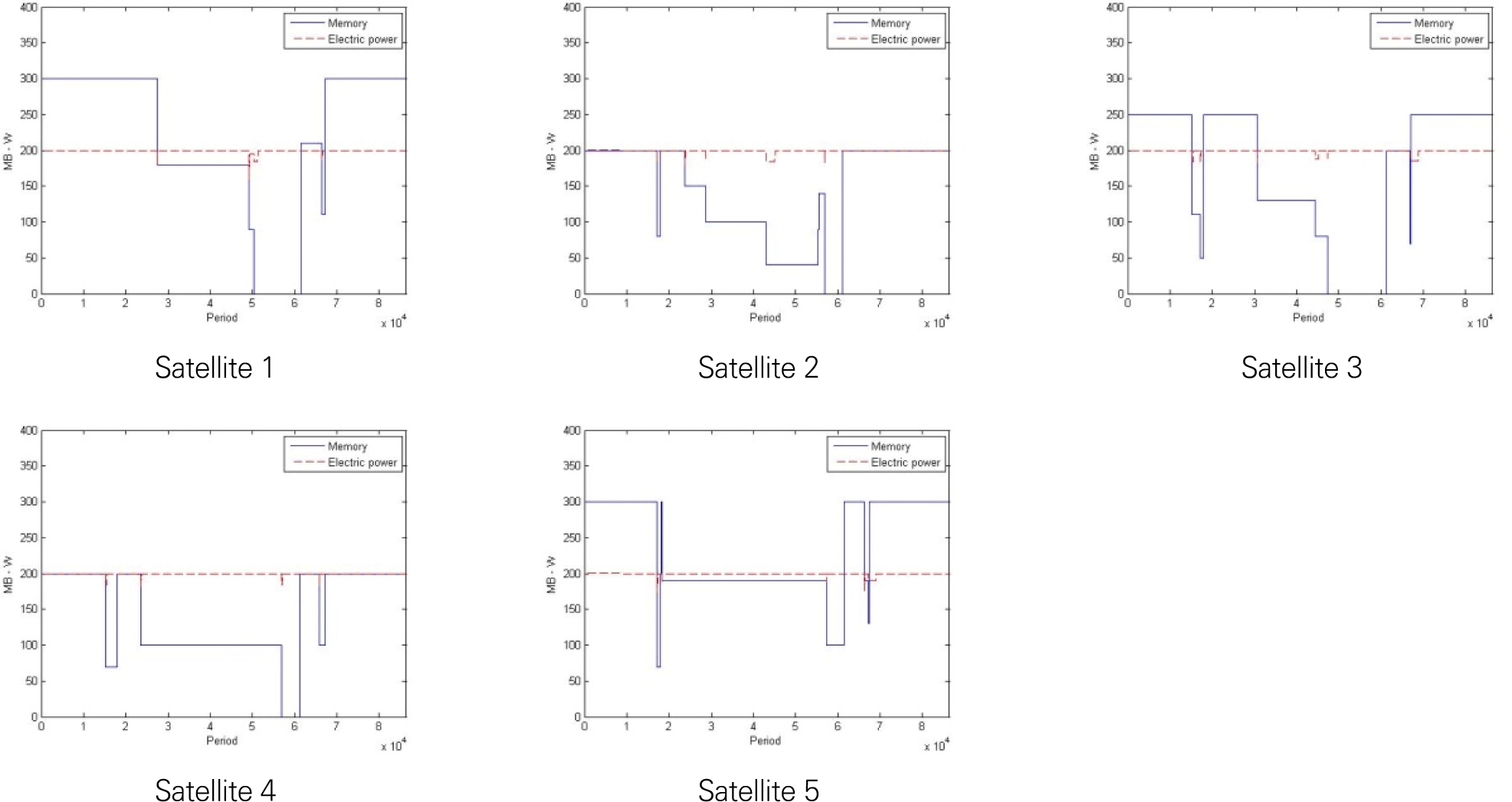
결론적으로 다중 위성 운영의 복잡한 스케줄링 문제를 해결하기 위한 GA 기반 접근법의 가능성을 입증하였다. 위성과 지상국 간 자원과 가시성 충돌을 통합적으로 고려한 설계가 주목할 만하다. 제안된 모델은 군사적 긴급 상황, 상업적 데이터 수집, 과학적 연구 등 다양한 공학적 문제 해결에 활용 가능성을 지닌다. 또한, 본 연구는 GA의 강력한 최적화 잠재력을 제시하며, 향후 더 복잡한 위성 시스템으로의 확장 가능성을 시사한다.

4.2 결정론적 접근법 - 혼합정수계획법

다중 위성과 다수의 지상국 간 임무 및 통신 스케줄링 문제를 최적화하기 위해 혼합정수선형계획법(mixed-integer linear programming, MILP)을 활용한 최적화 모델을 제안하였다[13]. 연구의 주요 목적은 제한된 자원과 시간 내에서 다중 위성과 지상국 간 상호작용을 최적화하여 임무와 통신의 효율성을 극대화하는 것이다.

MILP모델은 시간-공간 네트워크(time-space network, TSN)를 기반으로 스케줄링 문제를 수학적으로 정의하였다. TSN은 위성과 지상국 간의 가시권을 VTW(visibility time windows)로 정의하며 원격 명령 전송과 명령 수행 간의 시간적, 공간적 관계를 분석할 수 있도록 설계되었다. 이를 통해 위성 운영에서 발생할 수 있는 현실적인 제약 조건, 예를 들어 제한된 메모리 용량과 가시성 충돌을 통합적으로 반영한 최적화 문제를 효과적으로 해결하고자 하였다.

제안된 MILP 모델은 각 위성과 지상국의 동작을 수학적으로 표현하고, 명령 업링크, 데이터 전송, 이미지 저장 등 주요 작업을 시간 순서대로 계획하는 방식으로 설계되었다. 이 과정에서 위성과 지상국 간의 동시 수행 가능성(가시성 충돌)을 방지하며, 제한된 자원을 효율적으로 활용하도록 모델링하였다. 특히, 위성의 제한된 전력과 메모리 용량을 반영함으로써 현실적인 시스템 제약을 충실히 고려하였다.

한국 저궤도 위성군 데이터를 활용한 시뮬레이션을 통해 MILP 모델의 성능을 검증하였다. 그 결과 제안된 모델은 위성 활용도와 임무 성공률을 극대화하면서도 제약 조건을 만족하는 스케줄을 생성할 수 있음을 입증하였다. 특히, MILP 기반 접근법은 복잡한 스케줄링 문제를 체계적으로 분석하고 수학적으로 해결할 수 있는 강력한 도구임을 보여주었다.

5개의 임무에 대해 3개의 위성의 자윈(온보드 메모리)에 스케줄링된 결과는 Fig. 8과 같다. 계산은 1분 이내에 수행되었으며, 가시권을 포함한 상세 결과는 상기 논문에 나타나 있다.

Fig. 8. The scheduling results of on-board memory consumption [].

Download Original Figure

본 연구는 다중 위성과 지상국 간의 통합 스케줄링 문제를 해결하기 위해 정교한 수학적 모델링과 최적화 기법을 적용한 점에서 중요한 의의를 가진다. MILP 모델은 스케줄링의 복잡성을 줄이면서도 현실적 제약을 반영하였다.

4.3 비교

본 연구에서는 다중위성 영상운영 스케줄링 문제에 대해 두 가지 주요 최적화 접근법, 즉 GA를 활용한 추계적 방법과 MILP를 활용한 결정론적 방법을 비교하였다. 두 접근법은 상호 쌍대적 관계를 가지며, 각자의 강점과 한계를 가지고 있다.

GA의 주요 장점은 높은 적용성(applicability)이다. GA는 이산공간 및 비선형 모델과 같이 복잡한 형태의 최적화 문제에도 유연하게 적용 가능하다. 또한, 임무, 가시권, 제약 조건 등의 설계 변수가 증가하더라도 알고리즘 비용은 산술급수적으로 증가하기에 훨씬 많은 수의 임무 시뮬레이션을 수행할 수 있는 능력을 갖춘다. 또한, 염색체를 어떻게 설계하는가에 따라 상대적으로 더 복잡하고 대규모 모델에도 적용할 수 있다. 위 모델에서는 영상 촬영 시 전력 소모 및 복원(restoring)과 같은 세부적이고 복잡한 조건까지 고려할 수 있다. 그러나 GA의 한계는 도출된 해가 전역 최적해임을 보장하지 못한다는 점이다. GA는 준최적해를 탐색하고 이를 간접적으로 보여줄 수 있을 뿐, 전역 최적해에 대한 수학적 보증을 제공하지 못한다.

반면, MILP는 전역 최적해를 보장한다는 점에서 강력한 장점을 가진다. MILP는 선형 모델을 기반으로 설계되며, 제한된 메모리, 가시권, 데이터 전송 속도, 촬영 시퀀스와 같은 다양한 제약 조건을 정확히 반영한다. 그러나 MILP의 주요 한계는 적용성(applicability)이 낮다는 것이다. 선형 모델로 제한되기 때문에 비선형 모델이나 이산공간에 적용하기 어려운 경우가 많다.

또한, 임무 수와 변수의 증가에 따라 알고리즘의 계산 비용이 기하급수적으로 증가하며, 이는 대규모 문제에 대한 적용성을 제한한다.

결론적으로 GA는 높은 유연성과 대규모 문제에 대한 적용 가능성을 제공하는 반면, 전역 최적해에 대한 수학적 보증은 제공하지 못한다. 반대로, MILP는 전역 최적해를 보장하지만, 모델 유연성과 대규모 문제에 대한 효율성 면에서 제약을 가진다. 두 접근법은 각각의 문제 특성에 따라 선택적으로 적용될 수 있으며, 상호 보완적인 방식으로 활용될 수 있다. 두 연구의 상호 비교는 Table 2에 나타나 있다.

Table 2. Comparing approaches in case study

	MILP [13]	GA [11]
Imaging missions	5	50
Satellites	3	5
Resources and constraints	Memory capacity, visibility, data transmission rate, imaging mission sequence	Memory capacity, visibility, data transmission rate, imaging mission sequence, power consumption and restoring
Results	Maximize satellite resource utilization	Maximize user benefits in various resource constrains, operation modes, and missions
Algorithm complexity	High computational complexity, suitable for small-scale problems	Low computational complexity, suitable for large-scale simulations
Model applicability	Model flexibility limited to linear models	Can be applied and extended to nonlinear models, discrete spaces, etc.
Global optimality	Guaranteed global optimal solution	Able to approach near-optimal or global optimal solution

Download Excel Table

5. 결론

본 기고는 공학적 최적화와 설계 방법론을 체계적으로 탐구하고, 이를 적용하기 위한 결정론적 접근법과 추계적 접근법의 상호 보완성을 논의하였다. 물리적 현상 해석을 위해 목적 함수, 설계 변수, 제약 조건을 정의하며, 최적화는 비용과 효용을 고려한 설계의 핵심으로 작용한다. 결정론적 접근법은 볼록성과 KKT 조건을 기반으로 전역 최적해를 보장할 수 있다. 하지만 주로 선형 공간, 연속적이고 직교성을 갖는 변수에 적용 가능한 한계가 있다. 반면, 추계적 접근법은 유연성과 적용성이 높아 비선형 모델 및 이산공간 문제에서도 효과적으로 활용될 수 있다. 하지만 전역최적해에 대한 보증은 어렵다. 이를 바탕으로 다중위성의 영상 임무 운영에 적용한 case study를 소개하고 비교 분석하였다. 결론적으로, 두 접근법은 각각의 장단점을 가지고 있으며, 문제의 성격에 따라 선택적으로 적용되거나 상호 보완적으로 활용될 가능성이 크다. 이러한 연구는 공학적 최적화 기술의 이론적 기반을 제공하며, 향후 더욱 복잡한 시스템과 다양한 운영 조건을 해결할 수 있는 확장 가능성을 제시한다.

감사의 글

최적화 분야에 있어 조금이나마 너머를 바라볼 수 있도록 어깨를 내어 주신 연구자들께 감사드립니다.

References

Zeigler BP, Theory of Modeling and Simulation: Discrete Event & Iterative System Computational Foundations (Academic Press, London, UK, 2018).

Rao SS, Engineering Optimization: Theory and Practice (John Wiley & Sons, Hoboken, NJ, 2019).

Bathe KJ, Finite Element Procedures, 2nd ed. (Klaus-Jurgen Bathe, Hoboken, NJ, 2014).

Versteeg HK, An Introduction to Computational Fluid Dynamics the Finite Volume Method, 2/E 2nd ed. (Pearson Education India, London, UK, 2007).

Nocedal J, Wright SJ, Numerical Optimization (Springer-Verlag, New York, NY, 2006).

Arora JS, Introduction to Optimum Design (Elsevier Science, San Diego, CA, 2004).

Cormen TH, Leiserson CE, Rivest RL, Stein C, Introduction to Algorithms (MIT Press, Cambridge, MA, 2001).

Golberg DE, Genetic Algorithms in Search, Optimization, and Machine Learning (Addison-Wesley, Boston, MA, 1989).

Deb K, Multi-Objective Optimization Using Evolutionary Algorithms (John Wiley & Sons, Hoboken, NJ, 2010).

10.

Boyd S, Vandenberghe L, Convex Optimization (Cambridge University Press, Cambridge, UK, 2004).

11.

Lee J, Kim H, Chung H, Kim H, Choi S, et al., Schedule optimization of imaging missions for multiple satellites and ground stations using genetic algorithm, Int. J. Aeronaut. Space Sci. 19, 139-152 (2018).

12.

Lee J, Wang S, Chung D, Ko K, Choi S, et al., Scheduling optimization for image acquisition missions for multi-satellites via genetic algorithms, Korean Soc. Aeronaut. Space Sci. 951-957 (2012).

13.

Lee M, Yu S, Kwon K, Lee M, Lee J, et al., Mixed-integer linear programming model for scheduling missions and communications of multiple satellites, Aerospace. 11, 83 (2024).

Author Information

이 정 현jhlee16@kari.re.kr

jsta-5-1-47-i1

광주과학기술원 기전공학부에서 2016년 박사학위를 취득한 후 2019년부터 한국항공우주연구원에서 선임연구원으로 재직 중에 있다. 주 관심분야 및 전공은 스케줄링 최적화 및 시스템 자동화이며 위성 지상국의 실시간운영 및 임무계획 파트에서 지상시스템 개발, 운영 관리 업무 및 시스템 고도화 연구를 수행하고 있다.