Journal of Space Technology and Applications

The Korean Space Science Society

J. Space Technol. Appl. 2023; 3(3):229-238

pISSN: 2765-7469

DOI: https://doi.org/10.52912/jsta.2023.3.3.229

연구논문

차세대 중형 3호의 Magnetic Cleanliness Algorithm

최정림¹^,^†

, 이동렬²

, 이승욱¹

, 최두영¹

, 유광선³

Magnetic Cleanliness Algorithm for Satellite CAS500-3

Cheong Rim Choi¹^,^†

, Tongnyeol Rhee²

, Seunguk Lee¹

, Dooyoung Choi¹

, Kwangsun Ryu³

¹충북대학교 천문우주학과

²국가핵융합에너지연구원

³한국과학기술원 인공위성연구소

¹Department of Astronomy and Space Science, Chungbuk National University, Cheongju 28644, Korea

²Korea Institute of Fusion Energy, Daejeon 34133, Korea

³Satellite Technology Research Center (SaTRec), Korea Advanced Institute of Science and Technology, Deajeon 34141, Korea

^†Corresponding author : Cheong Rim Choi, Tel : +82-43-249-1616, E-mail : crchoi@chungbuk.ac.kr

© Copyright 2023 The Korean Space Science Society. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Jul 08, 2023; Revised: Aug 05, 2023; Accepted: Aug 10, 2023

Published Online: Aug 31, 2023

요 약

위성에서 나오는 자기잡음(magnetic noise)을 줄이는 것은 위성탐사에서 자력계의 성능을 향상시키는 중요한 방법 중의 하나이다. 자기잡음(magnetic noise)를 줄이는 방법 중의 하나가 위성에서 붐(boom)을 길게 뽑아내는 것이나, 이것은 높은 비용과 위성 운용 난이도 측면에서 선호하지 않는 방법이다. 그래서 많은 경우, 자기장 데이터 산출 후에 측정 데이터 세트에서 위성 플랫폼의 자기 간섭을 제거하는 것이 널리 사용된다. 본 연구에서는 붐 없이 태양전지판에 2개 그리고 본체 1개씩 각각 설치된 자력계(magnetometer)에서 관측한 자기잡음(magnetic noise)을 제거하는 알고리즘을 소개하고자 한다.

Abstract

One of the important ways to improve the performance of magnetometers in satellite exploration is to reduce magnetic noise from satellites. One of the methods to decrease magnetic noise is by extending the satellite boom. However, this approach is often not preferred due to its high cost and operational considerations. Therefore, in many cases, removing interference from the satellite platform in the measured dataset is widely utilized after data acquisition. In this study, we would like to introduce an algorithm for removing magnetic noise observed from magnetometers installed on two solar panels and one main body without a boom.

Keywords: 우주탐사; 위성 자력계; 자기 청소; 자기 잡음

Keywords: space exploration; satellite magnetometer; magnetic cleanliness; magnetic noise

1. 서론

2025년에 발사될 한국형 우주발사체인 차세대 중형위성(CAS 500-3)에 전리층 플라스마 관측 장비인 IAMMAP(Ionospheric Anomaly Monitoring by Magnetometer and Plasma-probe)이 탑재되며 IAMMAP은 day side 적도 지역에서 전리층의 플라스마 역학에 중요한 역할을 하는 EEJ(equatorial electro-jet)와 EIA(equatorial ionization anomaly) 사이의 상관 관계를 이해하기 위해 Impedance Probe, Langmuire Probe, 그리고 magnetometer인 AIMAG(adaptive in-phase magnetometer)로 구성되어 있다[1].

위성탐사에서 자기장관측은 우주환경 변화 및 연구에 매우 중요하다. 우주공간에서 우주환경이 변하는 것은 그곳에서의 플라스마 상태가 변하는 것을 의미하기 때문에, 그곳에서의 자기장의 현장관측(in situ)이 중요하다. 그래서 많은 위성에서 자력계를 탑재하여 여러 임무들을 수행해 왔다[2–5]. 위성 탐사 초기부터 정확한 자기장 측정을 수행하는 데 있어 주요 한계는 자력계 자체뿐만 아니라 탑재체를 운반하는 우주선에서 생성된 강한 잡음 자기장 때문이다. 이러한 잡음자기장을 줄이거나 제거하기 위하여 두 가지 종류의 자기청소 프로그램(magnetic cleanliness program)을 시행한다. 첫째, 위성 자력계에서 데이터를 얻은 이후, 자기 청소 절차를 거쳐 위성 플랫폼의 간섭과 전자기 방출을 효과적으로 제거할 수 있다. 이러한 방법은 시간과 비용 측면에서 가장 경제적인 방법이다. 둘째, 위성으로부터 붐을 전개하여 위성체 자기잡음의 영향을 줄이는 것이다. 이러한 붐의 전개는 대부분의 위성에서 사용하고, 자기잡음을 줄이기 위해 붐을 12 m까지 길게 전개한 위성[4]도 있지만, 1 m 정도로 짧게 전개한 GK2A(GeoKompsat-2A) 위성[6]도 있다. 뿐만 아니라 지상 자력계도 온도 및 여러 보정을 시행해서 자기 잡음을 줄여야 한다[7]. 이렇게 붐을 전개한 위성들도 소프트웨어적인 자기청소 프로그램(magnetic cleanliness program)을 수행하여야 한다[4–10].

본 연구에서 논할 자기청소 알고리즘(magnetic cleanliness algorithm)은 Constantinescu et al. (2020)[8]이 제시한 알고리즘으로서, Fig. 1과 같이 차세대 중형 3호(CAS500-3)에 붐 없이 태양전지판에 설치된 2개와 본체에 설치된 1개 자력계의 관측 차이를 이용하여 자기청소를 수행할 것이다.

Fig. 1. 차세대 중형 3호의 자력계 위치 개략도.

Download Original Figure

본 연구의 2장은 AIMAG의 간단한 디자인 및 구성에 관해 간략하게 다루고 있고 3장에서는 자기 청소의 한 방법인 principal component gradiometer algorithm에 관해 간단히 설명하고 4장에서는 1, 2, 3차 보정 matrix를 구하는 방법을 설명한다. 5장에서는 4장에서 구한 1차 및 고차 보정 행렬을 사용하여 인공적인 교란을 제거하는 결과를 간단히 보인다. 6장에서는 요약 및 결론에 관해 논의한다.

2. AIMAG(Adaptive In-Phase MAGnetometer) 프로토타입 디자인 (Design)

AIMAG는 링 코어 타입 플럭스게이트 자력계로 DC 자기장을 측정하기 위하여, 위성 태양 패널 양 끝에 각 1개, 그리고 위성 본체에 1개, 총 3개가 탑재될 예정이다[1]. AIMAG 플럭스게이트 자력계의 EQM 모델은 Fig. 2(a)와 같다. 각 유닛에는 3축 자기장 데이터를 얻기 위하여 1개의 링 코어가 2개의 축을 측정할 수 있기 때문에 1개의 자력계에 2개의 링 코어가 구성되어 있다.

Fig. 2. AIMAG 프로토타입 및 테스트 결과. (a) 플럭스게이트 프로토타입의 설계 사진, (b) X축 노이즈 레벨, (c) Y축 노이즈 레벨, 그리고 (d) Z축 노이즈 레벨. AIMAG, adaptive in-phase magnetometer.

Download Original Figure

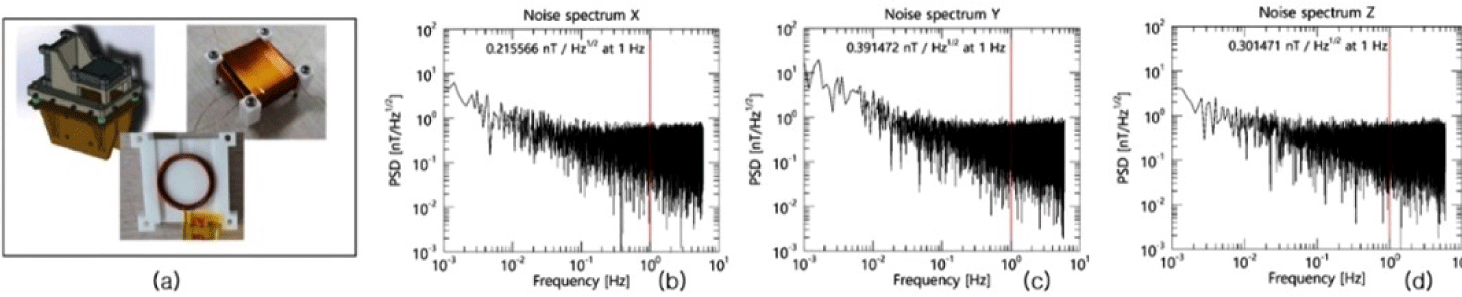
태양광 패널과 자력계 사이의 단열을 위해 열전도율이 0.4 W/m⋅K로 낮은 G10 소재로 만든 단열재를 자력계 지지대와 태양광 패널 사이에 설치한다. 자기장 측정의 성능을 결정하는 노이즈 특성은 주변 자기 교란을 1/1,000로 줄이는 자기 차폐 캔(TLMS-C100)에서 측정하였다[1]. Fig. 2(b)–(d) 215–390 pT/Hz의 잡음 수준으로 프로토타입 자력계에 대한 과학적 요구 사항을 충족하는 잡음 스펙트럼을 보여준다. 그러나 EQM 및 FM 개발 단계를 거쳐 곧 환경 테스트 및 정밀 정렬을 수행하여 성능을 향상시킬 계획이다.

3. The Principal Component Gradiometer Algorithm 원리

그라디오미터 기반 교란 청소 방법(gradiometer-based disturbance cleaning method)에 사용되는 일반적인 원칙은 두 개의 자력계를 갖고 서로 다른 지점에서 측정한 자기적인 차이를 이용하여 자기 잡음을 제거하는 것이다. 다시 말해, 위성에서 생성된 자기교란(magnetic disturbance)을 두 개의 자력계를 갖고 서로 다른 지점에서 측정한 자기적인 차이로 표현하는 것이다. 또한 위성에서의 자기교란(magnetic disturbance)이 거리에 따라 감소하고 주변 자기장(ambient magnetic field)을 변화시키지 않는다고 가정하고 자기 쌍극자(magnetic dipole) 기여만 고려한다.

i번째 자력계에서 측정한 자기장은 주변자기장(ambient magnetic field) $B ⇀ (t)$ 이고, 위성으로부터의 자기교란은 $∑ b ⇀ n i (t)$ 이고, 자기교란이 하나일 경우는 n= 1이다. i번째 자력계의 고유의 교란을 Zⁱ(t)라 하면, 다음과 같이 표현할 수 있다[6].

B 0, i (t) = B (t) + ∑ ​ b ⇀ n i (t) + Z i (t),

(1)

여기서 index 0는 초기에 측정한 자기장을 의미한다.

서로 다른 위치에 있는 두 대의 자력계에서 동시에 측정한 식 (1)을 서로 빼서 주변 자기장(ambient magnetic field)을 제거할 수 있다. 즉,

Δ B 0, i j (t) = B 0, i (t) − B 0, j (t) = ∑ ​ ​ Δ b n i j (t) + Δ Z i j (t),

(2)

와 같이 표현할 수 있다. 관측 데이터에서 자기교란장(magnetic disturbance)을 제거하기 위해, 각각의 자력계에서 ∆B^0,ij (t)의 선형결합(linear combination)용 교정계수(correct coefficient) $A k l i j$ 를 구해야 한다. 다시 말해,

B c o r r 0, i j (t) = B 0, i (t) + A i j Δ B 0, i j (t)

(3)

가 된다. 만일 자력계의 고유의 교란(specific disturbance)들을 무시하면, 식 (2)는

Δ B 0, i j (t) = Δ b i j (t)

(4)

가 된다. 이것은 자력계와 교란자(disturber)의 정확한 좌표를 알고 교란자(disturber)가 순수한 단일 쌍극자 또는 사중극자인 경우 계산할 수 있지만, 일반적으로는 측정에서 보정 행렬(correction matrix) A^ij를 직접적으로 구해야 한다.

4. 보정행렬

4.1 1차 보정(1^st Order Correction)

1차 보정 계수를 구하기 전에, 식 (2)의 첫째 항은 마지막 항보다 훨씬 크다고 가정한다. 이는 교란 소스 중 하나가 다른 것보다 자력계에 훨씬 더 강하거나 훨씬 더 가까운 경우에 해당된다. 이 경우 식 (4)와 같이 간단히 나타낼 수 있다. 센서 위치에서 교란의 방향을 찾으려면 자력계 위치에서 교란으로 인한 분산이 측정된 자기장의 최대 분산 방향을 결정한다고 가정한다. 이 경우 분산 분석을 통해 두 자력계 센서의 교란 방향을 추정할 수 있으며, 자력계 j의 측정값을 사용하여 보정된 자력계 i의 자기장의 구성 요소는 아래와 같이 VPS(variance principal system)에 쓸 수 있다[6].

B x 1, i j = B x 0, i j − α 0, i j (Δ B 0, i j) x,

(5a)

B y 1, i j = B y 0, i j,

(5b)

B z 1, i j = B z 0, i j,

(5c)

여기서 윗 첨자 "1"은 1차 보정을 의미한다. 식 (5)의 좌변과 우변의 첫 번째 항은 자력계 센서 i에서 측정값의 VPS로 표시되는 반면, 식 (5a)의 (∆B^0,ij)_x는 식 (5a)의 ∆∆B^0,ij의 VPS로 표현된다. VPS는 최대 분산을 x축으로 하고 최소 분산은 z축으로 맞추면 된다. 보정인자 α^0,ij의 계산은 측정값의 아래와 같은 분산으로 구할 수 있다. 즉,

α 0, i j = ± Var ((B 0, i) x) Var ((Δ B 0, i j) x),

(6)

여기서 ±부호는 VPS의 x축 방향이 분산 분석(variation analysis)에서 결정되지만 임의적이다. 만일 R^0,i가 자력계 센서 i에서 측정한 VPS까지의 센서 시스템에서 회전 행렬이고, R^0,ij가 ∆B^0,ij의 VPS에서 센서 시스템까지의 회전 행렬이면 센서 시스템에서 식 (5)는 다음 표현으로 나타낼 수 있다.

B k 1, i j = B k 0, i − α 0, i j ((R 0, i) − 1) k x (R 0, i j Δ B 0, i j) x

(7)

여기서 k=1,⋯,3이다. 이것을 matrix 형태로 나타내면,

B 1, i j = B 0, i + A 0, i j Δ B 0, i j

(8)

가 된다. 여기서 A는 교정 행렬로써

A k l 0, i j = − α 0, i j ((R 0, i) − 1) k x (R 0, i j) x l

(9)

이다.

4.2 고차 보정(Higher Order Corrections)

만일 식 (2)의 크기가 (혹은 절대값이) 예상한 지자기의 크기보다 일정 수준 이상이면, 추가적으로 보정을 반복적으로 적용할 수 있다. 차수 n − 1에서 차수 n까지의 반복적인 되풀이 관계식(iteration relation)은 다음과 같이 나타낼 수 있다.

B n, i j = B n − 1, i j + A n − 1, i j Δ B n − 1, i j; B 0, i j = B 0, i

(10)

여기서

A k l n − 1, i j = − α n − 1, i j ((R n − 1, i) − 1) k x (R n − 1, i j) x l

(11)

이다. 계수 α^n,ij는 차수 n까지 자기장의 분산에서 계산할 수 있고, 회전 행렬 R^n,i 및 R^n,ij는 n차 보정된 필드를 나타낸다.

식 (10)과 (11)을 사용하여, 두 개의 자력계 센서에서 측정한 값의 차이를 선형조합으로 표현한 결과, 다음의 2차 및 3차 보정된 자기장을 구할 수 있다.

B 2, i j = B 0, i + (A 0, i j + A 1, i j + A 1, i j (A 0, i j + A 0, j i)) Δ B 0, i j

(12)

그리고

B 3, i j = B 0, i + (A 0, i j + A 1, i j + A 2, i j + A 1, i j (A 0, i j + A 0, j i) + A 2, i j (A 0, i j + A 0, j i + A 1, i j + A 1, j i) + A 2, i j (A 1, i j + A 1, j i) (A 0, i j + A 0, j i)) Δ B 0, i j

(13)

센서 i에 대해 결정된 보정된 자기장 B^n,ij는 다음 센서를 포함한 비슷한 절차에서 측정된 필드 B^0,i를 대체할 수 있으며, 이러한 과정을 모든 센서의 측정값이 사용될 때까지 반복할 수 있다. 이상적으로는 하드웨어는 주 센서와 각 주요 간섭 원(major disturbance source) 근처에 위치한 센서로 구성되어야 한다. 그런 다음, 주 센서를 포함하는 각 센서 쌍에 대해서는 1차 보정만으로 데이터를 정제하는 것이 필요하지만 다른 센서 구성에도 사용할 수 있다.

5. 자기 잡음 제거

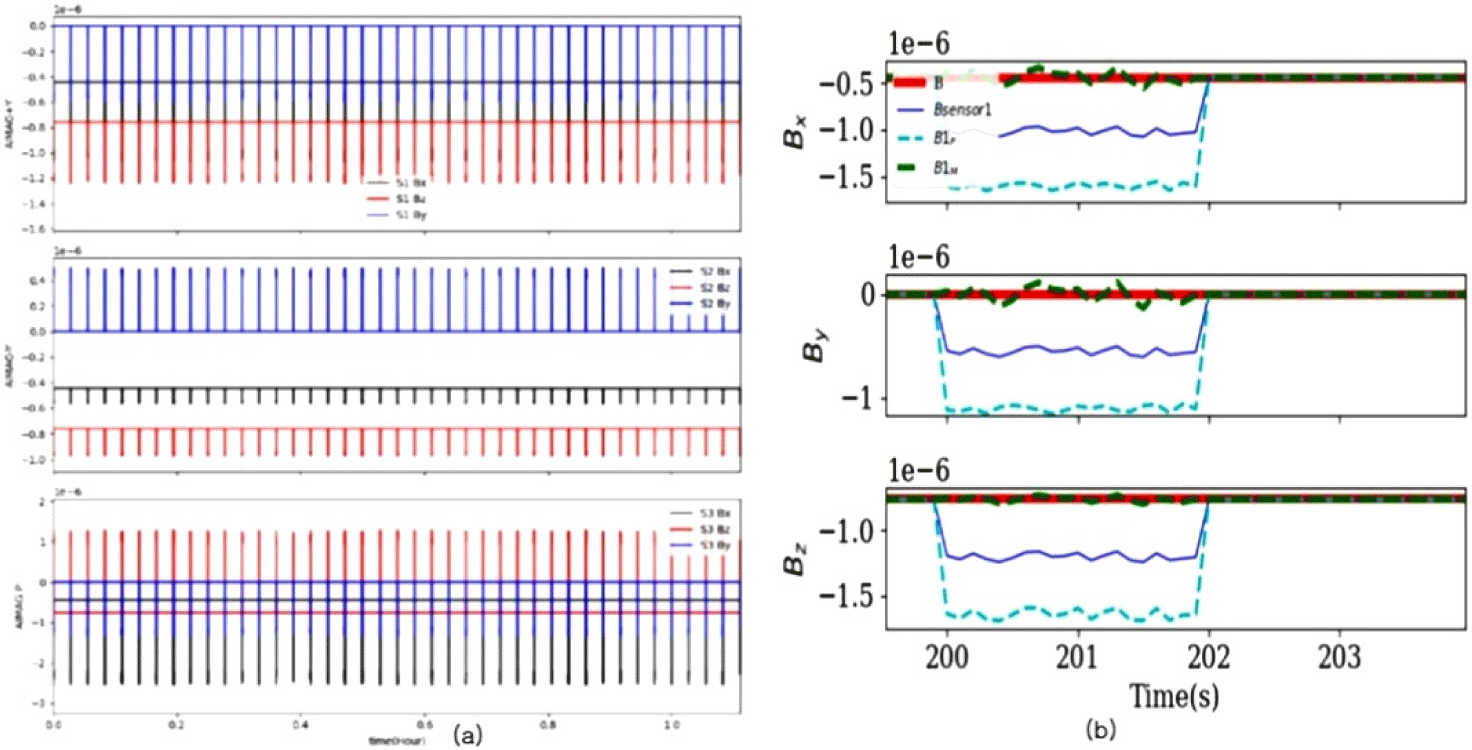
Fig. 3(a)는, 임의 고도에서의 위성 궤도운동을 각운동량 보존 법칙을 이용하여 계산한 후, 이 궤도에서 Fig. 3(b)처럼 지구 자기장을 순수 dipole 자기장으로 간주할 때, 자력계 센서 1(S1)과 2(S2)에서 관측(계산된)된 자기장이다.

Fig. 3. 지구자기장 시뮬레이션. (a) 임의의 고도에서 (b) 계산한 이상적인 dipole field.

Download Original Figure

이 자기장에 임의의 자기 모멘트(magnetic moment)의 세기가 M=(1,2,-7), 펄스 주파수가 f_pulse=0.01 H_z, 펄스 duration은 2s, 펄스 세기(pulse amplitude)는 0.1인 spike-like disturbance를 Fig. 4(a)와 같이 생성하여 더해 주었다. Fig. 4(a)와 같은 spike-like 자기 잡음이 주기적으로 들어오는 경우, Fig. 4(b)와 같이 임의의 구간(200–202s)의 spike-like 자기 잡음을 1차 교정 행렬을 이용해서 제거(녹색)한 것이다. 파란색은 센서 1에서 관측한 자기 잡음이고 하늘색은 식 (6)에서 +를 선택하여 얻어진 결과이다.

Fig. 4. Spike-like type noise 제거. (a) Pulse 주파수 0.01 Hz, pulse duration 2s인 spike-like 인공 교란, (b) 199–204s 구간에서 1차 교정 후 인공 교란 제거한 결과.

Download Original Figure

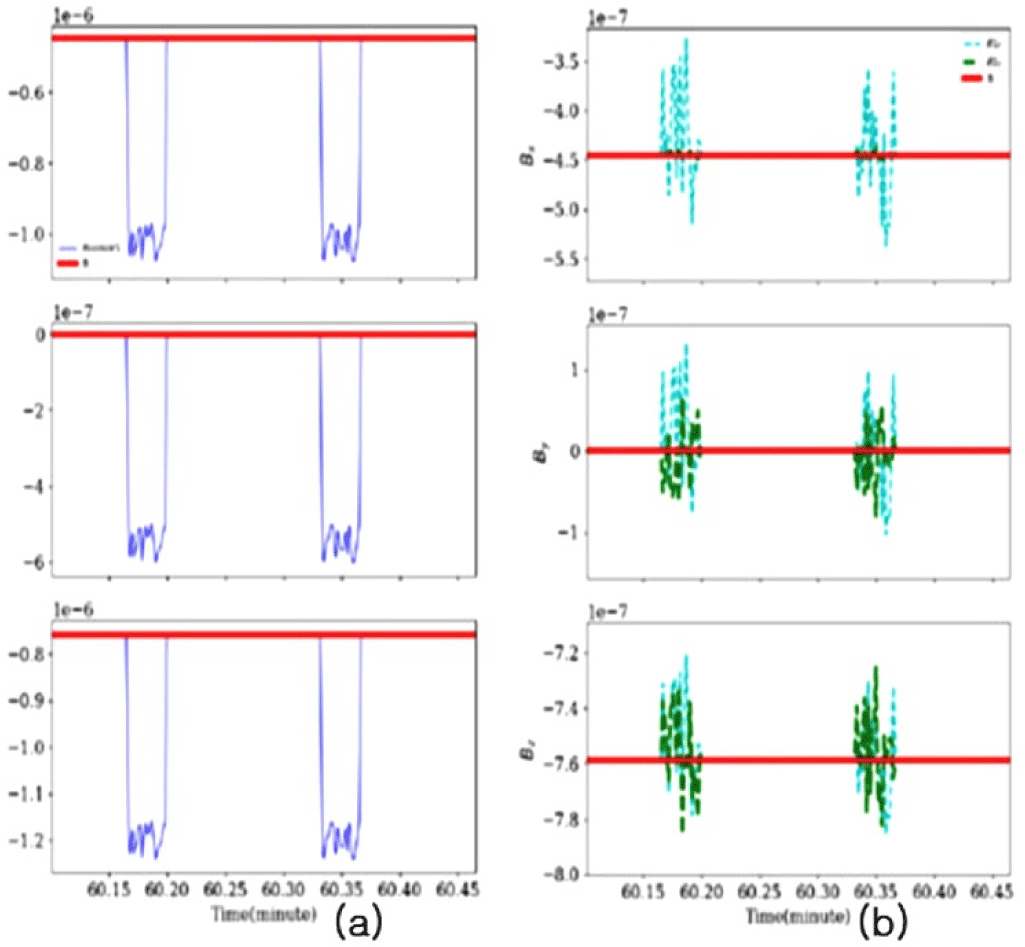
이렇게 spike-like 자기 잡음도 1차 보정으로 제거되지 않는 경우도 있다. 예를 들어, Fig. 5(a)에서는 1차 보정 후 여전히 남아 있는 잡음을 볼 수 있으며, 이것을 2차 보정을 시행하여 Fig. 5(b)처럼(녹색) 많은 부분을 제거할 수 있다. 또한, 2차 보정을 시행하여 남아 있는 잡음을 3차 보정 시행으로 많은 부분의 잡음을 줄일 수 있다. Fig. 6은 2차 3차 보정의 예로써, 노이즈 주파수가 0.1 Hz인 step-like 형태의 노이즈를 발생시켰고 9,000s 윈도우로 나타냈다. Fig. 6(a)는 2차 보정을 했지만 여전히 자기 잡음이 남아 있었고, Fig. 6(b)에서 3차 보정 후, 자력계 센서 1에서 관측한 연두색(식 (6)에서 + 적용) 데이터는 잡음이 많이 포함되어 있지만,센서 2에서 관측한 녹색의 데이터(식 (6)에서 + 적용)는 대부분의 잡음이 제거가 되어 붉은색에 접근함을 볼 수 있다.

Fig. 5. 2차 보정의 예: (a) 1차 보정 후 남아 있는 노이즈, (b) 2차 보정 후 노이즈 상태. 하늘색은 센서 1에서 관측한 데이터를 의 plus로 2차 보정한 결과이고, 녹색은 센서 2에서 관측한 데이터를 의 plus로 2차 보정한 결과이다.

Download Original Figure

Fig. 6. 3차 보정의 예. (a) 2차 보정 후 데이터, (b) 3차 보정 후 데이터.

Download Original Figure

6. 요약 및 결론

본 연구에서는 Fig. 1에서와 같이 차세대 중형 3호(CAS500-3)에 설치된 3대의 플럭스게이트 타입 자력계를 이용하여 gradiometer 방법으로 자기 청소(magnetic cleanliness) 방법을 연구하였다. 위성에 붐없이 설치된 자력계들의 경우에 유용하게 적용할 수 있다. Fig. 4(a)처럼 인공적인 spike-like 잡음을 주파수 0.01 Hz, duration 2초로 발생시켰다. Fig. 4(b)에서는 (a)에서 만든 인공적인 자기장교란을 1차보정 행렬을 사용하여 제거한 결과이다. 녹색과 붉은색(지구 자기장)이 잘 일치함을 볼 수 있다. 결과적으로 1차 보정만 시행해도 대부분의 spike-like 자기잡음(magnetic noise)는 제거 가능하다. 하지만, Fig. 5, 6과 같은 step-like 형태의 잡음은 2, 3차 등 고차 보정을 해야 대부분의 잡음이 제거됨을 볼 수 있다. 또한 식 (6)에서처럼 보정 행렬의 부호는 임의적이어서 정확한 방향성이 없는 것을 확인하였다. 지금까지의 자기 잡음은 인공적으로 만들어서 제거하였지만, 앞으로 실재적인 자기 잡음이 포함된 위성에서 관측한 자기장 데이터를 갖고 여러 고차 보정까지 시행하여 자기 잡음을 제거할 계획이다.

감사의 글

이 연구는 과학기술정보통신부가 지원하는 한국연구재단(NRF)의 위성개발사업(NRF-2021M1A3A4A06086639)의 지원으로 수행되었습니다. 저자들은 CAS500-3 임무와 KSLV 개발에 참여한 엔지니어들에게 특별한 감사를 표합니다.

References

Ryu K, Lee S, Woo CH, Lee J, Jang E, et al., Technical paper: science objectives and design of ionospheric monitoring instrument ionospheric anomaly monitoring by magnetometer and plasmaprobe (IAMMAP) for the CAS500-3 satellite, J. Astron. Space Sci. 39, 117-126 (2022).

Behannon KW, Acuna MH, Burlaga LF, Lepping RP, Ness NF, et al., Magnetic field experiment for voyagers 1 and 2, Space Sci. Rev. 21, 235-257 (1977).

Dougherty MK, Kellock S, Southwood DJ, Balogh A, Smith EJ, et al., The Cassini magnetic field investigation, Space Sci. Rev. 114, 331-383 (2004).

Escoubet CP, Schmidt R, Goldstein ML, Cluster - science and mission overview, Space Sci. Rev. 79, 11-32 (1997).

Ludlam M, Angelopoulos V, Taylor E, Snare RC, Means JD, et al., The THEMIS magnetic cleanliness program, Space Sci. Rev. 141, 171-184 (2008).

Kato M, Sasaki S, Takizawa Y, The Kaguya Project Team, The Kaguya mission overview, Space Sci. Rev. 154, 3-19 (2010).

Choi D, Lee S, Kim J, Lee DY, Choi KC, et al., Development of thermostat for the fluxgate magnetometer in icheon geomagnetic observatory and stability evaluation after installation, J. Space Technol. Appl. 2, 221-229 (2022).

Constantinescu OC, Auster HU, Delva M, Hillenmaier O, Magnes W, et al., Principal component gradiometer technique for removal of spacecraft-generated disturbances from magnetic field data, Geosci. Instrum. Methods Data Syst. (2020).

Jo HJ, Jin H, Park H, Kim KH, Jang Y, et al., Analysis of a cubesat magnetic cleanliness for the space science mission, J. Space Technol. Appl. 2, 41-51 (2022).

10.

Lee J, Sohn J, Park J, Yang TY, Song HS, et al. SNIPE mission for space weather research, J. Space Technol. Appl. 2, 104-120 (2022).

Author Information

최 정 림crchoi@chungbuk.ac.kr

jsta-3-3-229-i1

부산대학교 물리학과에서 2002년에 박사를 취득하여 현재 충북대학교 천문우주학과에서 우주플라스마연구를 하고 있다. 차세대 중형 위성 3호의 위성용 자력계 제작 및 magnetic cleanliness program에도 참여하고 있다.

이 동 렬trhee@kfe.re.kr

jsta-3-3-229-i2

포항공과대학교 물리학과에서 학사, 석사, 박사를 마치고 현재 국가 핵융합연구원에서 책임연구원으로 근무하고 있다.

이 승 욱lsu1080@gmail.com

jsta-3-3-229-i3

충북대학교에서 2015년 천문우주학 학사학위를 받고, 같은해 동대학원에 석박사통합과정에 입학해 2019년 수료하였다. 현재 차세대 중형 위성 3호 우주과학 탑재체의 플라즈마 검출기와 자기장 측정기 개발을 담당하고 있다.

최 두 영atlas4604@naver.com

jsta-3-3-229-i4

충북대학교 천문우주학과에서 2022년 석사학위를 취득하였으며, 2022년부터 충북대학교 박사과정에 있다. 현재 위성 탑재용 자기장 측정 장비 개발에 참여하고 있으며, inner heliosheath에 대해 연구하고 있다.

유 광 선kwangsun@kaist.ac.kr

jsta-3-3-229-i5

KAIST 물리학과에서 2000년에 박사를 취득하여 현재 KAIST 인공위성연구소에서 우주플라즈마 및 과학탑재체 관련 연구를 수행하고 있다. 2025년 발사예정인 차세대중형위성 3호의 과학탑재체인 IAMMAP(Ionospheric Anomaly Monitoring by Magnetometer And Plasma-probe: 플라즈마 관측기 및 자력계)의 연구책임자를 역임하고 있다.