1. 서론
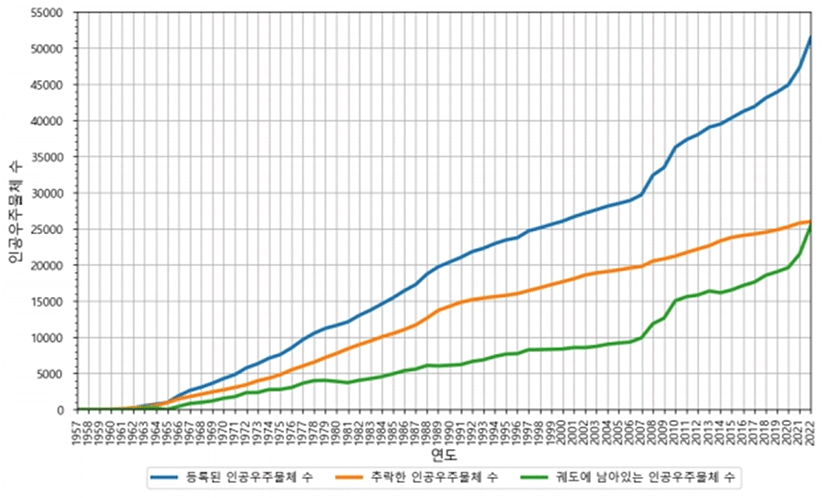
우주 위험은 지구나 인간의 우주 활동에 직, 간접적으로 위협이 되는 지구 주변의 우주 환경을 의미한다. 우주 위험은 크게 추락과 충돌로 인한 위험으로 구분되며, 자연우주물체와 인공우주물체에 의해 발생한다. 우주물체의 추락 위험은 소행성, 유성체와 같은 자연우주물체 혹은 수명이 다한 인공위성, 발사체 잔해와 같은 인공우주물체가 지구로 추락하면서 전소되지 않아 지상에 피해가 발생하는 경우, 충돌 위험은 우주잔해물과 운영 중인 인공위성 혹은 인공위성과 인공위성 간의 충돌로 위성 운영에 일시적 장애가 발생하거나 중단되는 경우를 말한다. 이러한 우주 위험의 원인들 중 인공우주물체는 인류의 우주 개발과 함께 그 숫자가 지속적으로 증가하고 있어 이로 인한 위험성 역시 점점 커지는 상황이다. 지구 궤도상의 인공우주 물체는 2007년 중국의 풍운 1호(FY-1C) 위성 요격 실험, 2009년 미국의 통신용 이리듐 위성과 러시아의 군통신용 코스모스 위성 간의 충돌로 급격히 증가한 바 있다. 2021년 11월에는 러시아의 코스모스 1408 위성 요격 시험으로 1,500여 개의 파편을 발생시키기도 했다. 또한 초대형군집위성군 중 미국 스페이스 X의 스타링크(Starlink)는 2019년 5월 24일 첫 발사 이후, 2022년 2월까지 2,044여 개를 발사하며 우주물체의 증가를 가속시켰다. Fig. 1은 지구 궤도상의 인공우주 물체 수 그래프로 2007, 2009년의 급증 외에도 최근 2년 이내 저궤도 인공우주물체의 증가세가 가속되는 것을 확인할 수 있다[1].
이와 같은 인류의 활발한 우주개발 및 우주물체 간 연쇄충돌로 근 지구 우주환경이 점점 복잡해지면서 우주상황인식(space situational awareness, SSA)과 우주교통관제(space traffic management, STM)에 대한 관심도 높아지고 있다. 우주상황인식은 지상과 우주의 관측장비를 통한 우주물체의 관측과 분석을 통한 대응 활동을 포함하며 우주 환경에 대한 포괄적인 지식의 획득과 이해를 의미한다[2]. 우주교통관제는 우주상황인식을 기반으로 우주공간의 안전한 활용과 우주운용을 위한 일련의 기술 및 규제를 의미한다[3]. 우주상황인식과 우주교통관제를 위한 모듈중 우주위험 분석 시스템은 관측을 통해 수집된 데이터를 분석하여 우주물체 재진입 위험이나 근접우주물체에 대한 충돌확률을 계산하여 우주위험도를 판단하게 한다
미국의 연합우주작전본부(Combined Space Operation Center, CSpOC)는 우주상황인식의 주요 정보제공자로 우주감시네트워크(space surveillance network)를 통해 획득한 우주감시 및 추적 등 우주물체의 궤도 정보와 근접 경고 메시지(conjunction data message, CDM)를 제공하고 있다. 각 기관이 운영하고 있는 우주자산에 타 우주물체가 근접할 경우 위성운영기관에 근접경고메시지를 보내주고 있다. CDM의 경우 CSpOC의 고정밀 궤도력을 활용한 결과를 담고 있지만, 일반적인 추적 정보는 정밀도가 낮은 관측평균궤도정보인 TLE(two line element)로 제공되며, 군사 및 안보와 관련된 민감한 정보는 제외되어 있다. 우주물체의 궤도 정밀도는 우주위험 분석에 직접적인 영향을 끼치기 때문에 세계적으로 우주활동이 증가하는 상황에서 궤도력의 정밀도를 높이는 것은 더욱 중요해졌다. 따라서 우주 자산 보호를 위해서는 정밀 궤도력 확보가 필요하며, 이를 통한 우주위험 통합 분석시스템 구축이 필수적이다[4]. 우리나라는 우주위험대비 기본계획을 바탕으로 독자적인 우주위험을 분석할 수 있는 역량 확보를 위한 우주물체 관측시스템과 우주위험 통합분석 시스템을 개발 중이며, 본 연구 또한 그 일환으로 수행되었다.
본 연구에서는 우주물체 간 충돌위험 분석을 위한 기존 방법론들을 분석하였고, 이를 바탕으로 다양한 관점에서 우주물체 간 충돌위험을 분석하기 위한 이중 모드 프레임워크를 제안하였다. 제안된 프레임워크는 두 물체 간 기하학적 관계를 바탕으로 일대일 충돌 위험도를 분석하는 미시적 모드(microscopic mode)와 관심 물체가 통과하는 공간에서 발생하는 평균 충돌 횟수를 바탕으로 충돌 위험도를 산출하는 거시적 모드(macroscopic mode)로 이루어져 있으며, 유효성 검증을 위해 각 모드에 적합한 사례 연구가 수행되었다.
2. 우주물체 충돌 위험 분석 기법 및 프로그램
지구 궤도 상 우주물체의 밀도가 급격히 증가함에 따라 충돌 위험이 점점 커지고 있으며, 이러한 위험을 정확히 파악하기 위한 대응 시스템 및 핵심 기술에 대한 연구가 활발히 진행중이다. 본 장에서는 기존의 충돌 위험 분석 방법론들과 해외 기관에 의해 개발된 충돌 위험 분석 프로그램 현황을 서술하였다. 기존의 충돌 위험 분석 기법은 크게 두 물체 간의 기하학적 관계를 이용하는 방법과 관심 영역의 충돌 플럭스(collision flux)를 활용한 기법으로 나뉘어지며 각각 2.1, 2.2절에 서술하였고, 2.3절에서 충돌 위험 분석 프로그램에 대한 현황을 서술하였다.
일대일 충돌 위험 분석은 주 관심 대상(primary object)과 잠재적 위험 대상(secondary object) 두 물체 간 기하학적 관계를 이용하여 위험도를 분석하는 기법이다. 일대일 충돌 위험 분석을 위한 기하학적 관계가 Fig. 2에 제시되어 있다. 대표적인 충돌 위험 지표로는 두 물체 간 거리가 최소가 되는 지점(point of closet approach, PCA) 및 시점(time of closet approach, TCA)과 이 때의 상대 거리인 최근접거리(miss distance) 등이 있으며, 최근접거리가 기준거리보다 가까워지는 경우를 충돌(collision), 그 확률을 충돌 확률(probability of collision, PC)이라고 정의한다. 우주물체 간 거리가 가까워져 충돌 위험이 발생할 때 이와 같은 지표들을 반복적으로 계산하는 과정을 충돌 위험 분석 혹은 충돌 평가(conjunction assessment, CA)라고 한다. 일반적으로 충동확률이 10–4보다 큰 경우, 추가적인 분석 혹은 충돌 회피 기동이 필요한 위험 케이스로 분류되며, 보다 정확한 위험분석과 의사결정을 위해 반복적인 재관측과 이를 통한 궤도 결정이 수행되어야 한다.
충돌 확률 계산과정에서 두 물체의 상태에 대한 불확실성은 공분산(covariance) 행렬을 통해 나타낼 수 있다. 공분산 행렬의 대각 성분은 각 파라미터의 분산이며, 그 외의 성분은 두 파라미터의 표준편차와 상관계수(correlation coefficient)의 곱으로 표현된다. 우주물체 간 충돌분석 과정에서 공분산 행렬은 주로 위성 중심의 UVW 좌표계에서 표현되며, U와 W는 각각 위성의 공전 중심 방향과 각 운동량의 방향, V는 W와 U 방향 단위벡터의 외적방향으로 정의된다. 공분산 값은 궤도 결정 과정에서 관측 오차 및 동역학 모델의 불확실성을 고려하여 생성되고, 몬테 카를로(Monte Carlo), 선형 맵핑(linear mapping), 시그마 포인트 전파(Sigma point propagation) 기법 등을 활용하여 위험 분석 시점에서의 값을 얻을 수 있다.
두 우주물체 간 충돌 확률은 식 (1)과 같이 구할 수 있으며, C 는 두 물체의 공분산의 선형 합, V 는 두 물체를 감싸는 구의 부피 합, r 은 두 미소 부피 요소 간 위치 벡터를 의미한다. 이와 같은 3차원 충돌 확률 계산법은 직관적이지만 많은 계산 비용이 요구되기 때문에 이를 보완한 방법론이 다양한 연구자들에 의해 제안되었다.
Foster는 두 물체의 충돌 평면(encounter plane)을 활용한 충돌 확률 계산법을 다음과 같이 제안하였다.
Foster의 충돌확률 계산법은 이후 개발된 충돌확률 계산법에 비해 많은 계산 비용이 필요하지만, 3차원 계산법과 비교하였을 때 정확성에 큰 차이가 없으며, 적분 간격 조절을 통해 계산 속도를 높일 수 있다. Foster 방법론은 STK(systems tool kit)의 ODTK(orbit determination tool kit) 충돌 분석, space-track에서 배포하는 CDM, NASA의 충돌 위험 분석 프로그램 CARA 등에 활용되고 있다.
Chan의 Foster가 제안한 충돌 확률 계산식의 해석적인 근사해를 다음과 같이 제시하였다.
Chan은 2차원 가우스 확률 밀도 함수를 1차원 Rician 확률 밀도 함수로 변환하였고, 등가 영역(equivalent area) 개념을 이용한 해석해를 제안하였다. Chan의 방법론은 ISS의 충돌 회피 기동 의사결정 지원에 사용되고 있으며, 각 물체의 크기가 1–100 m, 두 물체 간 거리가 10 m–100 km, 위치에 대한 표준 편차가 1–10 km인 상황에서 활용이 권장된다.
Patera는 3차원 충돌확률 문제를 밀도 대칭 가정을 활용해 1차원 선적분 형태로 표현하였다. r 과 q 는 두 물체의 확률분포 중심과 물체 간 거리와 방향을 나타내며, 확률분포 중심이 물체에 포함되지 않는 경우 식 (4)와 같이, 포함되는 경우 식 (5)와 같이 충돌 확률을 표현할 수 있다. Patera의 방법론의 Aerospace Corporation사의 collision vision tool, satellite orbit analysis program 등 포함한 다양한 기관에서 활용 중이다.
Alfano는 충돌 확률 산정 문제의 복잡도를 줄이기 위해 몇 가지 가정을 세웠다. 1) 두 물체를 각각 대상을 포함하는 구체로 가정하여 자세 정보 없이 충돌 확률을 계산하였다. 2) 두 물체 간 상대 가속도가 상대 속도에 비해 매우 작다고 가정함으로써 두 물체 간 상대 속도를 선형으로 가정하였다. 3) 두 물체의 위치는 Zero-mean, 가우시안(Gaussian) 분포를 따르고, 서로 비상관(uncorrelated) 관계이며 충돌분석 기간 중 일정하다고 가정하였다. 4) 두 물체가 비상관 관계이기 때문에 두 물체 간 충돌 기하를 Fig. 3과 같이 결함 공분산 타원체(combined covariance ellipsoid)와 결합 구형 물체(combined spherical object)로 표현할 수 있고, 타원체와 구형 물체가 맞닿을 때 충돌이 발생한다고 가정하였다. 위 가정들을 바탕으로 선형으로 가정한 상대 속도에 수직인 충돌 평면(encounter plane)에 3차원 공분산 타원체와 구형 물체를 사영시켜 2차원 문제를 치환하였으며, 충돌 확률을 다음과 같이 표현하였다.
충돌 플럭스 기반 충돌 위험 분석 방법론은 관심 대상의 궤도가 통과하는 공간에 초점을 맞추어 위험 대상 물체들이 해당 공간에 발생시키는 공간밀도(spatial density)를 바탕으로 충돌 확률을 산출한다. 본 세부 절에서는 관심 궤도의 평균 충돌 플럭스를 산정하고, 이를 통한 충돌 확률 계산 방법론에 대해 서술하였다.
1단계는 분석 대상 공간을 구면 좌표계 상에서 Radial 방향(Dri), Declination 방향(Ddj), RAAN 방향(Dak)으로 나누어 Δri×Δαk×Δδj 크기 셀(cell)로 쪼개는 과정이다. 각 셀의 크기는 인덱스 i, j, k로 조절할 수 있으며, 각 셀의 중심을 나타내는 위치 벡터는 식 (7), 부피는 식 (8)과 같이 계산할 수 있다.
각 셀을 공간 밀도는 셀을 통과하는 우주물체가 해당 셀에 존재할 확률을 바탕으로 계산할 수 있다. 먼저 임의의 우주물체가 특정 셀을 통과하는 시점의 진근점이각(true anomaly)은 각 축 방향에 따라 radial 방향은 식 (9), declination 방향은 식 (10), RAAN 방향은 식 (11)과 같이 계산되며, 그 시점은 식 (12)와 같이 계산된다.
n 은 위험 대상 물체에 대한 인덱스(counter for a debris object), m 은 이 물체의 한 주기 동안 발생하는 셀 통과 이벤트에 대한 인덱스(cell passage event counter along a single orbit of this object), l 은 셀 (i, j, k)를 통과하는 모든 위험 대상 물체에 대한 인덱스(counter for all orbit passes of a given debris population through one particular cell)라고 할 때, 위험 대상 물체가 셀에 머무는 시간(Dtl(i, j, k))은 식 (13)과 같이 계산할 수 있다.
이때 해당 물체의 주기에 대한 통과 시간 비율을 통해 특정 셀에 존재할 확률을 식 (14)와 같이 구할 수 있으며, 셀의 부피에 대한 비율을 통해 식 (15)와 같이 밀도를 표현할 수 있다. 따라서 총 밀도는 셀을 통과하는 모든 위험 물체 l(i, j, k) = 1, K, Ll,j,k 의 밀도 합으로 식 (16)과 같이 표현된다.
관심 궤도의 플럭스는 대상이 통과하는 각 셀의 부피와 공간밀도 정보를 바탕으로 구할 수 있다. l 번째 위험 물체로 인해 m 번째 셀에 생성되는 플럭스(Fm,l)는 식 (17)과 같이 표현된다.
여기서 Pm 은 관심 대상이 셀 m 에 존재할 확률, Dl 은 위험 물체 l 로 인한 밀도, Dnm,l 은 셀 m 에서 관심 대상과 위험 물체 l 간의 상대속도이다. 관심 궤도의 전체 플럭스는 식 (18)과 같이 표현할 수 있고, 기체 분자 운동론(the laws of kinetic gas theory)에 따라 평균 충돌 횟수(c)를 식 (19)와 같이 표현할 수 있다.
Ac는 관심 대상의 단면적, Dt 충돌 위험 분석 기간을 의미한다. 우주물체 간 충돌은 매우 낮은 확률로 발생하기 때문에 충돌 사건을 푸아송 분포로 가정하면 분석 기간 중 충돌이 n 번 발생할 확률, 1번 이상 발생할 확률을 각각 식 (20), (21)과 같이 표현할 수 있다.
CARA는 NASA에 의해 개발된 충돌 위험 분석 프로그램으로 NASA의 우주 임무들을 보조하기 위해 18th Space Control Squadron(18SPCS)에 구축되었다. CARA 운영팀은 잠재적 충돌 위험을 감시하고 평가하며 위성 소유, 운영자(owner/operator, O/O)의 충돌 회피 기동에 대한 의사결정 과정을 지원한다. Fig. 4는 CARA의 운영 프로세스를 나타낸다.
첫 번째 단계인 CA는 high accuracy catalog(HAC)를 활용해 보호 자산의 궤적을 검증하여 충돌을 예측하는 것이다. 이 단계는 CARA orbital safety analysts(OSA)에 의해 수행되며, 두 가지 형태의 궤적 정보를 사용한다. 하나는 분석 기간 중 계획된 기동을 포함하는 O/O가 제공한 궤적이며, 다른 하나는 계획된 기동에 대한 정보가 없는 DoD 우주 감시 네트워크의 추적 데이터를 바탕으로 한 궤적이다. 두 궤적을 바탕으로 한 분석 결과는 지구 저궤도 물체의 경우 하루에 3번, 그 외의 경우 하루 2번 기록된다. 두 번째 단계는 궤도 분석 결과를 바탕으로 한 위험 평가 단계이다. CARA는 데이터를 처리하고 업데이트된 동향 정보를 O/O에게 전송하는 자동화된 시스템(connection assessment system, CAS)을 보유하고 있다. 이후 CARA 팀은 고위험으로 간주되는 케이스들에 대한 추가적인 충돌 위험 분석을 수행한다. 마지막 세 번째 단계는 충돌 회피로, 위험 완화 전략의 계획 및 실행을 지원한다.
ESA에서 제공하는 MASTER 프로그램은 자연 및 인공 우주물체 정보를 활용한 특정 궤도의 우주물체 밀도와 충돌 플럭스(collision flux) 정보를 제공한다. MASTER 프로그램에서 사용하는 인공 우주물체 데이터베이스는 인공위성 및 충돌로 인한 잔해, 발사체 상단, 고체 부스터 등 추적 가능한 물체들과 페인트 조각, 추진제의 잔해 등 관측이 불가능한 물체에 대한 모델링 기반 데이터가 포함되어 있다. 자연 우주물체 모델은 Divine-Staubach, Cour-Palais, Jenniskens/McaBride, GRUN 모델 등을 활용하여 구축되어 있다.
MASTER 프로그램에서는 지구의 저궤도부터 달의 고궤도 구간에 대한 우주물체 밀도와 플럭스 정보를 제공하며, 임의의 Delta-Walker Pattern 인공위성군을 데이터베이스에 추가하여 분석을 수행할 수 있다.
국내에서도 한국천문연구원과 한국항공우주연구원을 중심으로 우주물체 충돌 위험 분석을 위한 연구들이 수행되어 오고 있다. 한국항공우주연구원에서는 충돌 위험 분석을 위한 프로그램인 KARISMA(KARI Space debris collision risk MAnagement system)를 개발하여 운용하고 있다[12].
3. 충돌 위험 분석을 위한 이중 모드 프레임워크
기존의 충돌 위험 분석 방법론들과 해외 기관에 의해 개발된 충돌 위험 분석 프로그램 현황 분석을 바탕으로 본 연구에서는 우주물체의 충돌위험 분석을 위한 이중 모드 프레임워크가 제안되었다. 제안된 이중 모드 프레임워크의 개념도가 Fig. 5에 제시되어 있다. 제안된 프레임워크는 두 물체 간 1:1 충돌 이벤트에 초점을 맞춘 미시적 모드(microscopic mode)와 특정 공간에서 발생하는 평균 충돌 횟수에 초점을 맞춘 거시적 모드(macroscopic mode)로 구성되어 있다.
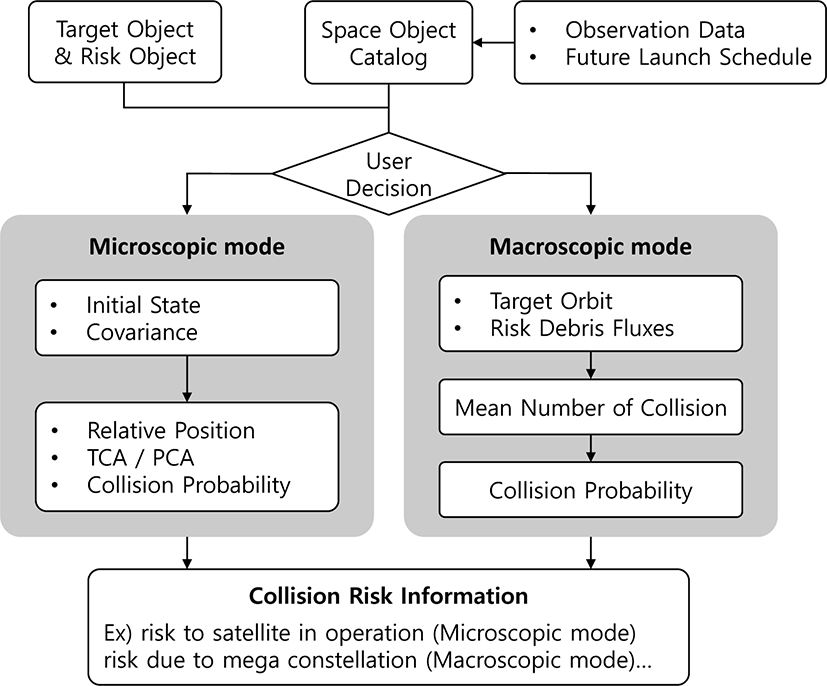
미시적 모드의 경우, 관심 대상(target object)과 충돌 가능성이 있는 위험 물체(risk object)들에 대해 각각 일대일 충돌위험 분석을 수행한다. 두 물체 간 충돌 위험도는 기하학적 관계와 위치에 대한 불확실성을 나타내는 공분산 행렬에 의해 결정되며, 두 물체의 최근접 지점 및 시점과 시간에 따른 충돌확률을 얻을 수 있다. 미시적 모드는 짧은 기간에 대해 정밀한 분석을 수행할 때 활용할 수 있으며 궤도정보와 함께 각각의 물체에 대한 불확실성 정보가 요구된다. 제안된 프레임워크의 미시적 모드 구현에는 Foster 방법론[5]이 활용되었다.
거시적 모드의 경우, 관심 대상의 궤도가 통과하는 공간에 초점을 맞추어 충돌위험을 분석한다. 먼저 전체 공간을 셀로 나눈 후, 관심 대상이 통과하는 셀을 도출한다. 이후 관심 대상이 통과하는 각 셀에 대하여, 특정 셀을 통과하는 물체들과 관심 대상의 상대 속도를 이용하여 각 위험 물체들이 생성하는 충돌 플럭스를 산정한다. 이를 바탕으로 각 셀의 플럭스를, 전체 궤도에 대한 플럭스를 얻을 수 있으며, 분석 기간 중 평균 충돌 횟수 및 충돌확률을 계산할 수 있다. 거시적 모드 구현에는 ESA에서 개발한 MASTER 프로그램이 활용되었다.
미시적 모드의 경우, 관심 대상과 위험 물체가 특정되는 경우 비교적 짧은 기간에 대한 분석에 적합하며 시간에 따른 두 물체 간 충돌 위험 분석을 통해 최근접 시점 및 충돌 회피 기동 여부를 결정할 수 있다. 이와 같은 분석으로 신뢰도 높은 위험 분석 결과를 얻기 위해선 두 물체의 상태, 크기, 공분산에 대한 정확한 정보가 요구된다. 하지만 일반적으로 우주물체의 정밀한 정보를 얻는 것은 쉽지 않다. Space-track에서 제공하는 TLE 형식의 데이터베이스도 존재하지만 이는 최대 수 km의 위치오차를 가진다고 알려져 있으며 공분산 값을 제공하지 않는다. 반면, 거시적 모드는 공분산 값이 요구되지 않고 상태정보에 대한 위험 분석의 결과 민감도도 상대적으로 낮다. 또한 장기간 분석을 수행하는 경우, 미시적 모드에 비해 계산비용을 단축할 수 있다. 거시적 모드를 활용한 장기간 분석과 미래 우주 환경에 대한 시뮬레이션은 향후 임무 설계 단계에서 위성이 겪는 충돌 위험 수준을 파악하고, 미래의 우주물체 분포를 예측할 수 있다.
기존 충돌 위험 관련 연구들의 경우, 특정 상황에 적합한 방식에 대한 연구가 주를 이룬다. 본 연구에서는 기존 방법론들에 대한 분석을 바탕으로 우주물체 간 충돌 위험 전반을 다루기 위한 프레임워크를 제안하였다. 활용가능한 정보의 수준과 분석 목적에 따라 서로 상호 보완적 특성을 가지는 두 가지 충돌 분석 방법론 중 적합한 방법을 택하여 위험도 정보를 도출하도록 하였다. 미시적 모드에 해당하는 충돌 분석 방법론의 경우, 현재 위성 운영기관에서 임무 운영 단계에, 거시적 모드에 해당하는 방법론은 임무 설계 단계에서 주로 활용되고 있다. 하지만 임무 설계 단계에서도 효율적인 충돌 회피 궤적 설계를 위해 일대일 충돌 상황에 대한 해석 즉, 미시적 모드가 활용될 수 있다. 또한 운영 단계에서도 주변에 새로운 초대형 위성군이 전개되는 상황에서 거시적 모드를 활용해 연간 예상 충돌 횟수를 재계산하고, 이를 바탕으로 향후 임무 계획 수정을 지원할 수 있다.
4. 사례 연구
본 절에서는 제안된 프레임워크의 효용성 검증을 위한 사례 연구가 수행되었다. 세부 1,2절에서는 미시적 모드를, 3절에서는 거시적 모드를 활용한 사례 연구 및 결과를 서술하였다.
본 사례 연구는 COSMOS 1275의 파편과 FENGYUN 1C의 파편 간 충돌위험 분석을 수행하였다. 고도 약 880 km에 위치하는 두 물체의 TLE를 활용한 위험분석 결과를 Spacetrack 웹사이트에 공개된 Public Conjunction 메시지와 비교하였다. 두 가지 궤도 전파 모델(SGP4, Spherical-harmonic)을 활용하여 TCA 및 Pc를 계산하였고, 그 결과를 Table 1 및 Fig. 6에 제시하였다. TCA의 경우, 두 가지 전파 모델 모두 public conjunction 메시지의 TCA와 1초 이내 결과를 보였지만 최소 근접 거리와 충돌확률에 차이를 보였다. Spacetrack의 경우, 충돌 위험 분석시 TLE가 아닌 내부 정밀 궤도력을 사용하는 것으로 알려져 있으며, 본 사례 연구의 결과에 나타난 충돌확률 차이의 원인으로 추정할 수 있다. 미시적 분석 모드의 경우, 우주물체 간 충돌확률은 두 물체 간 거리, 두 물체의 크기, 관측값의 오차 수준에 의해 결정된다. 이와 같이 특정 충돌 사건 분석에는 궤도정보가 위험 정보를 도출하는 데 있어 매우 중요하게 작용한다. 본 사례 연구는 충돌 위험 분석 역량을 향상시키고, 예측 정확도를 높이기 위해 신뢰도 높은 데이터의 확보가 매우 중요함을 보여준다.
| Space-track | SGP4 | Spherical-harmonic | |
|---|---|---|---|
| TCA (UTC) | 2021-10-08 | 2021-10-08 | 2021-10-08 |
| 07:31:02.387 | 07:31:02.374 | 07:31:02.296 | |
| Min distance (m) | 21 | 264.88 | 626.20 |
| Pc (–) | 7.35475e-04 | 0 | 0 |
미시적 모드를 활용하여 충돌 위험 분석을 수행하는 경우, 관측 정보의 정밀도 수준을 나타내는 공분산 값은 충돌 확률을 결정하는 주요 변수 중 하나이다. 충돌 확률은 두 물체 간 거리가 작을수록, 각 물체의 크기가 클수록 증가하는 반면, 공분산의 변화에 대해서는 단조 증가 형태가 아닌 특정 시점에서 다시 감소하는 형태를 보인다. 이러한 경향으로 인해 위험 분석에 사용된 공분산 값에 따라 같은 충돌 확률 값을 가지더라도 의사결정이 달라지는 경우가 발생한다. Fig. 7은 KOMPSAT3A 위성과 STARLINK 2228 위성 간의 CDM을 바탕으로 공분산 및 위성 크기에 따른 충돌 확률 변화를 나타낸다. 상대거리가 두 물체의 크기(hard body radius, HBR)보다 큰 경우, 관측 정보의 정밀도가 높아짐에 따라 즉, 공분산이 작아짐에 따라 충돌 확률이 0으로 수렴하는 구간을 robust region, 충돌 확률이 커지는 구간을 dilution region이라고 부른다[13]. 본 사례연구에 사용된 공분산 값은 robust region에 속하지만 공분산 값이 변할 경우 충돌확률이 최대 100배 정도까지도 증가할 수 있다.
Fig. 8은 임의의 두 물체에 대한 공분산 크기에 따른 충돌 확률 변화 그래프로, 이러한 Dilution Effect를 설명하고 있다. 충돌 위험 판단 확률 기준을 10–3이라 할 때, 공분산 값이 C2, C3가 주어진 경우에는 동일한 충돌 확률을 보이며 두 경우 모두 기준을 초과하여 위험한 케이스로 판단할 수 있다. 공분산 값이 C1으로 주어진 경우는 충돌 확률이 기준 이하로 안전한 케이스이며 상대적으로 작은 값의 공분산을 가져 관측 신뢰도가 높은 경우로 최종적으로 안전한 상황이라고 판단할 수 있다. 하지만 공분산 값이 C4로 주어지는 경우는 충돌 확률만 보았을 땐 기준 이하이지만 공분산 값이 상대적으로 크기 때문에 관측 신뢰도가 낮은 상황으로 재관측이나 궤도 결정 모델의 개선을 통해 공분산 값이 낮아지면 충돌 확률이 높아지는 Dilution Region에 속한다. 이와 같은 경우에는 충돌 확률이 기준 이하이더라도 안전한 상황으로 판단할 수 없으며 추가적인 분석을 통한 의사결정이 필요하다.
충돌 위험 분석 및 의사결정 과정에서 충돌 확률은 가장 직관적으로 위험도를 나타내는 지표이다. 하지만 본 사례연구를 통해 충돌 확률이 절대적인 기준이 될 수 없음을 보였고, 분석 과정에서 사용된 변수들을 포함한 종합적인 판단의 중요성을 알 수 있다.
본 세부 절에서는 거시적 충돌 위험 분석 모드를 통해 저궤도 위성의 충돌 위험도를 분석하였다. 타겟 위성은 고도 550 km 태양동기궤도에 위치한 단면적 3 m2의 물체로 가정하였고, 위성군은 같은 고도에 위치한 SpaceX Starlink를 Lower-shell을 가정하였다. Starlink 위성군은 53도의 궤도경사각과, 72개의 궤도 평면, 각 궤도 평면당 22개의 위성이 위치한 Delta-Walker 패턴으로 가정하였다. Starlink의 유무에 따른 위성의 1년간 플럭스, 평균 충돌 횟수, 1번 이상 충돌이 발생할 확률을 Table 2와 같이 정리하였다.
크기가 10 cm 이하인 우주물체들에 대한 충돌위험의 경우 위성군 유무에 따른 차이가 크게 나타나지 않았지만 1 m 이상 물체에 대한 위험의 경우 위성군이 없는 경우에 비해 충돌확률이 4배 이상 커짐을 확인할 수 있다. Fig. 9는 1–100 m 크기의 물체들에 대한 고도별 플럭스를 나타낸 그래프로 위성군으로 인한 플럭스 증가를 확인할 수 있다.
Table 3은 위성군의 단면적과 개수 변화에 따른 충돌 위험 분석을 수행한 결과이다. 전체 위성의 숫자가 줄어들면 플럭스 및 충돌 확률이 감소함을 확인할 수 있다. 반면 위성의 크기가 커질수록 실제 충돌 확률은 증가하지만 거시적 모드에 활용된 방법론의 특성상 이러한 영향이 반영되지 않음을 확인할 수 있다.
5. 결론
인류의 우주개발이 시작된 이후 지구궤도의 우주물체 수는 꾸준히 증가해 왔으며, 위성간 충돌, 위성 요격 실험, 초대형 위성군 임무 증가로 인해 증가세가 가속화되고 있다. 이에 따라 우주물체의 추락 및 충돌 위험 대응 기술에 대한 중요성도 점점 높아지고 있다. 본 연구에서는 기존의 우주물체 간 충돌 위험 분석 방법론들을 검토하고, 이를 바탕으로 한 이중 모드 프레임워크를 제안하였으며, 사례 연구를 통해 그 효용성을 확인하였다.
제안된 이중 모드 프레임워크는 두 물체 간 일대일 충돌 사건에 초점을 맞춘 미시적 모드와 관심 궤도가 지나는 공간에 초점을 맞춘 거시적 모드로 구성되어 있다. 미시적 모드는 두 물체의 궤도 및 크기 정보와 궤도 정보의 불확실성을 나타내는 공분산 값을 통해 충돌 위험을 분석하기 때문에 신뢰도 높은 정보 하에 위험 분석 및 의사결정이 수행되어야 한다. 충돌 위험도를 분석하기 위한 지표로는 두 물체의 최 근접 지점 및 시간, 최소 근접 거리, 충돌 확률 등이 있다. 충돌 확률은 충돌 위험도를 직관적으로 표현할 수 있어 여러 기관에서 의사결정 기준으로 활용되고 있다. 하지만 우주물체의 위치 공분산으로 크기로 인한 충돌 확률의 dilution 효과로 인해 최소 근접거리나 충돌 확률만으로는 우주물체의 충돌 위험을 단정할 수 없음을 확인할 수 있었다. 따라서 분석 과정에서 사용한 변수들을 포함한 종합적 판단되어야 한다는 것을 사례연구를 통해 확인하였다.
초대형 군집위성의 급격한 증가로 저궤도 영역이 붐비고 있다. 향후 5년, 10년 이후의 저궤도 영역의 밀집도와 이로 인한 우주물체 간의 충돌 위험 증가 등 미래 우주환경 분석을 위해서는 거시적 모드의 분석이 필요하다. 특정 사건에 대한 분석으로 충돌 회피기동 여부를 판단하는 경우에는 미시적 모드로 분석하여야 하지만, 미래 우주 환경 예측과 충돌 위험 증가 분석에는 거시적 모드 분석이 되어야 한다. 이는 위성의 안전한 운용을 위해 위성의 임무 설계 단계에서의 운영 궤도 선택과 위성의 보호 전략 등에 반영되어야 한다. 본 연구에서는 1년간의 임무 분석을 수행하였지만, 수십년 이상의 기간에 대한 충돌 위험 분석에도 유용하게 활용된다. 이와 같은 장기간 충돌 분석에는 지구 궤도 우주 물체에 대한 다양한 모델링이 요구되며, 향후 연구에서는 우주 물체의 연쇄 충돌 및 다양한 위성 전개 시나리오를 고려한 미래 환경 예측과 이에 따른 충돌 위험도 분석을 수행하고자 한다.
점점 복잡해지는 근 지구 환경으로 인해 우주 상황 인식 및 우주 교통 관제에 대한 중요성이 커지고 있다. 본 연구에서 제안된 이중 모드 프레임워크는 주어진 정보와 상황에 따른 적합한 충돌 위험 정보를 도출할 수 있으며, 이를 활용하여 우주물체 충돌위험 대응을 위한 우주위험 대비 체계 구축에 기여할 수 있을 것으로 기대한다.




















