Design of Inertial Navigation System/Celestial Navigation System Navigation System for Horizontal Position Estimation and Performance Comparison Between Loosely and Tightly Coupled Approach

Kim, Kiduck

doi:10.52912/jsta.2023.3.1.58

J. Space Technol. Appl. 2023; 3(1):58-71

pISSN: 2765-7469

DOI: https://doi.org/10.52912/jsta.2023.3.1.58

연구논문

수평 위치정보 추정을 위한 관성/천측 항법시스템 설계 및 약결합/강결합 방식의 성능 비교

김기덕 ¹ ^, ^†

Design of Inertial Navigation System/Celestial Navigation System Navigation System for Horizontal Position Estimation and Performance Comparison Between Loosely and Tightly Coupled Approach

Kiduck Kim ¹ ^, ^†

Author Information & Copyright ▼

¹한국항공우주연구원

¹Korea Aerospace Research Institute, Daejeon 34133, Korea

^†Corresponding author : Kiduck Kim, Tel : +82-42-860-2978, E-mail : KiduckKim@kari.re.kr

© Copyright 2023 The Korean Space Science Society. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Dec 12, 2022; Revised: Dec 27, 2022; Accepted: Jan 06, 2023

Published Online: Mar 31, 2023

요 약

본 논문에서는 관성측정장치와 천측 항법을 활용한 수평 위치 추정을 위한 항법 시스템 설계에 대해 기술하였다. 우주 상에서 별은 천구 상에 널리 퍼져 있는 천체로서 별의 관측을 통해 자세 정보를 획득하는데 주로 사용되어 왔다. 하지만 별의 고도 정보를 통해 수평 위치에 대한 정보 또한 획득이 가능한데, 이는 천측 항법이라고 불리며 예전 항해사들이 바다 위 항해 중에 자기의 위치를 알아내던 원리와 동일하다. 특히 GPS 등의 사용이 불가능한 심우주에서는 비교적 관측이 쉬운 별을 통해 위치에 대한 정보를 획득하는 것이 중요하다. 따라서 본 논문에서는 수평 위치정보를 추정할 수 있는 항법 시스템을 소개하며 측정값을 활용하는 방식에 따라 약결합과 강결합의 두 가지 방식의 시스템을 설계하고자 한다. 시뮬레이션을 통해 설계된 시스템이 올바르게 수평 위치정보를 추정하는지 여부와 함께 약결합과 강결합 방식의 성능을 비교하여 추후 천측 항법을 활용한 항법 시스템 설계에 도움이 되고자 한다.

Abstract

This paper describes a navigation system design for horizontal position estimation using inertial measurement sensors and celestial navigation. In space, stars are widely spread objects in the celestial sphere and have been used mainly to obtain attitude information through star observation. However, it is also possible to obtain information about the horizontal position with the altitude of the star. It is called celestial navigation which is the same principle that former navigators used to locate themselves while sailing on the sea. In particular, in deep space where GPS is not available, it is important to obtain information on the location by making use of stars that are relatively easy to observe. Therefore, we introduce a navigation system that can estimate horizontal position and design two types of systems, loosely coupled and tightly coupled depending on how the measurements are utilized. It is intended to help in the future design of navigation system using celestial navigation by simulation studies that not only verify whether the system correctly estimates horizontal position but also comparing the performance of loosely and tightly coupled methods.

Keywords: 수평 위치; 관성측정센서; 천측 항법; 항법 시스템; 약결합; 강결합

Keywords: horizontal position; inertial measurement sensor; celestial navigation; navigation system; loosely coupled; tightly coupled

1. 서론

우주 탐사에서 정확하고 신뢰성 있는 단독적(autonomous)인 항법 시스템은 비행체의 생존을 보장하고 맡은 바 임무를 완료할 수 있는 핵심적인 기술이다[1]. 그러나 GPS 등은 근지구에서만 사용이 가능하거나, 지상 추적 방식의 경우 통신 지연이나 갑작스런 통신 두절의 문제가 발생할 수 있기 때문에 효과적으로 단독 항법 시스템을 구성하기 어렵다.

일반적으로 사용되는 단독 항법은 관성 항법 및 천측 항법 등이 있다. 먼저 관성 항법은 각속도계 및 가속도계 등의 관성 센서를 사용하여 선형 각속도 및 가속도를 측정하며, 이러한 측정값을 통합하여 자세, 위치, 속도 등을 외부 도움 없이 획득할 수 있다. 그러나 관성 센서 들은 짧은 시간에 높은 정밀도를 가지지만 시간에 따라 오차가 흐르는(drift) 성징을 가지고 있어 그 오차가 빠르게 증가한다[2]. 반면에 천측 항법은 천체를 관측함으로써 시간에 관계없이 자세 혹은 위치에 대한 항법 정보를 동시에 제공할 수 있다[3]. 따라서 관성 항법과 천측 항법은 오차 누적 방식에서 상호 보완적이라고 할 수 있다.

본 논문에서는 천측 항법을 통해 수평 위치를 획득하는 방안에 대하여 소개하고 해당 값을 관성 항법과 함께 활용할 수 있는 항법 시스템에 대하여 기술한다. 이를 위하여 천측 항법으로부터 상태변수와 동일한 형태의 수평 위치를 그대로 사용하는 약결합 방식과 별의 고도 정보를 사용하는 강결합 방식 두 가지 시스템을 설계한다. 또한, 시뮬레이션을 통해 설계한 항법 시스템에 대한 분석과 함께 약결합과 강결합 두 가지 방식의 결과를 비교하여 추후 천측 항법을 포함하는 항법 시스템 설계에 활용할 수 있도록 한다.

2. 천측 항법(Celestial Navigation)

천측 항법은 기본적으로 별의 관측을 통해 항법 정보를 획득하는 것을 의미하며 자세 정보만을 보정하는 경우[4]와 위치 정보를 보정하는 경우[5] 두 가지로 나뉘게 된다. 물론 위치 정보를 위해서는 별의 관측뿐 아니라 해당 별의 고도에 대한 측정이 필요하지만, 비교적 관측이 쉬운 별을 통해 위치에 대한 정보를 획득할 수 있는 경우 시스템의 초기화 등 항법의 단독성을 보장하는데 큰 장점이 된다.

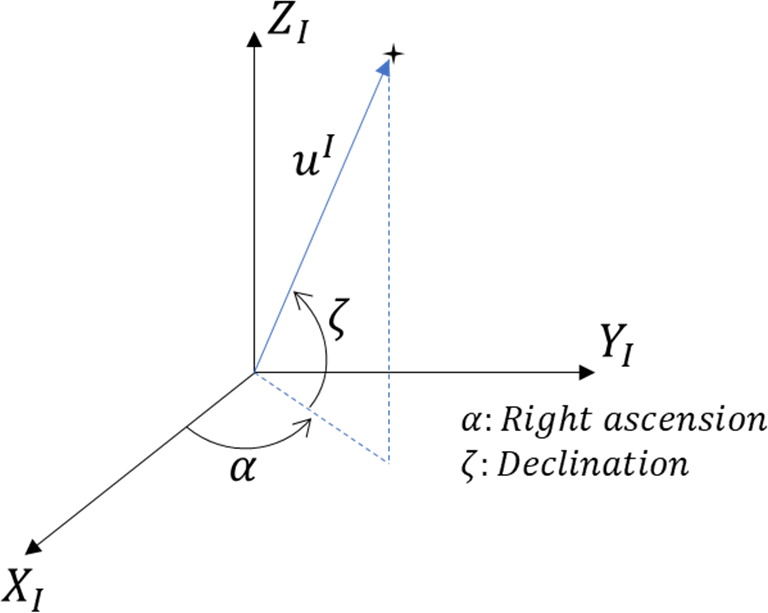
천측 항법에서는 기 알려진 별의 적경(right ascension)과 적위(declination)에 대한 정보와 함께 추가적으로 별의 고도를 측정하여 관측자의 위도 및 적도 등의 수평 위치를 알아내게 된다. Fig. 1은 관성 좌표계에서 관측된 별의 벡터 u^I를 나타내며, α 및 ζ는 각각 별의 적경과 적위를 나타낸다.

Fig. 1. Star observation vector.

Download Original Figure

이 때 관측 벡터 u^I는 식 (1)과 같이 나타낼 수 있다.

u I = [cos α cos ζ sin α cos ζ sin ζ]

(1)

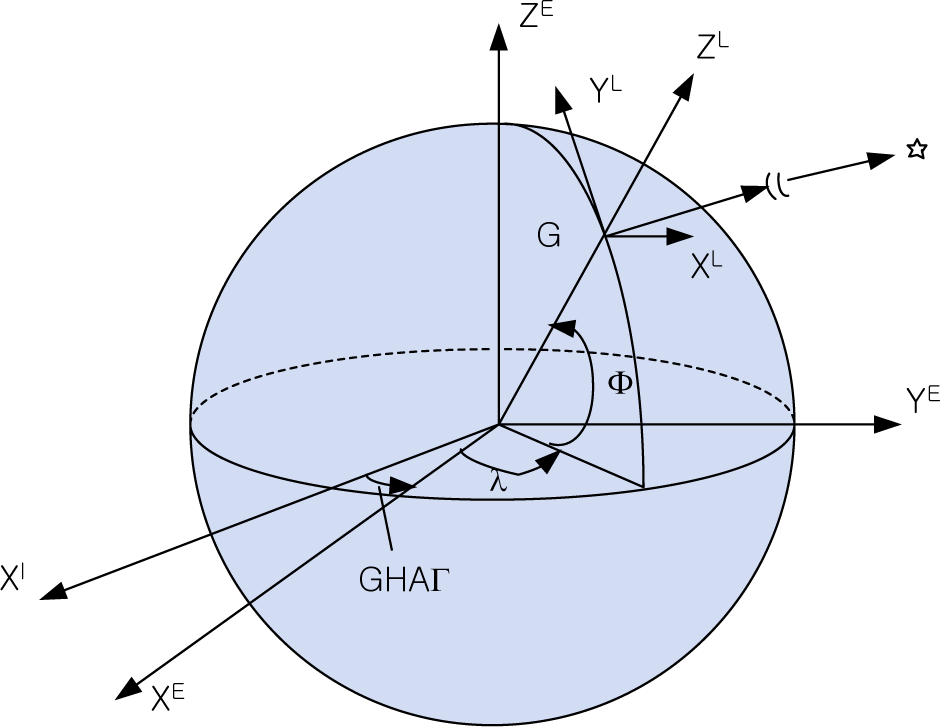
만일 관측된 별을 아래 Fig. 2와 같이 지면 좌표계에 대하여 표현한 벡터를 u^L이라 할 경우 방위각(azimuth)와 고도각(elevation)을 통해 식 (2)와 같이 표현할 수 있다.

Fig. 2. Local frame geometry.

Download Original Figure

u L = [cos A z cos E l sin A z cos E l sin E l]

(2)

벡터 u^I와 u^L 사이의 관계는 좌표계 사이의 자세변환행렬을 통해 계산이 가능하다.

u L = C E L C I E u I

(3)

각각의 자세변환행렬은 아래와 같이 정의된다.

C I E = [cos (G H A) − sin (G H A) 0 sin (G H A) cos (G H A) 0 001]

(4)

C E L (E N U) = [− sin λ − sin φ cos λ cos φ cos λ cos λ − sin φ sin λ cos φ sin λ 0 cos φ sin φ]

(5)

여기서 Greenwich Hour Angle은 천체의 시간각을 의미하며, φ 및 λ는 각각 관측자 혹은 비행체의 위도와 경도를 의미한다. 식 (3)에 식 (2), (4), (5)를 대입하여 정리할 경우, 세 번째 항으로부터 아래의 식 (6)을 정리할 수 있다. 이 식은 LOP(line of position) 식이라고 불리며 천측 항법에서 활용되는 가장 주요한 식으로 별의 고도와 관측자의 위도와 경도 사이의 관계를 의미한다. LOP 식이 가진 물리적 의미는 지면 상에서 동일한 고도를 가진 수평 위치를 나타내며, 이를 만족하는 해를 알아내는 방식은 여러 가지가 있다[6,7]. 그러나 본 논문의 주요한 내용은 이를 통해 알아낸 수평 위치를 활용하는 항법 시스템에 대하여 기술하는 것으로 여러 방식들에 대한 자세한 설명은 포함하지 않는다.

sin E l = sin φ sin ζ + cos φ cos ζ cos (α − G H A − λ)

(6)

본 논문에서는 LOP 식을 활용한 최소자승법을 통해 수평 위치를 계산한다. 먼저 구하고자 하는 값 x를 아래와 같이 위도 φ와 경도 λ에 대한 행렬로 정의한다.

x = [φ, λ] T

(7)

이 때, 익히 알려져 있는 식 (8)과 같이 새로운 x를 업데이트하여 해를 찾게 된다.

x k + 1 = x k + (A T A) − 1 A T Δ y

(8)

여기서 ∆y는 LOP 식을 통해 아래와 같이 계산할 수 있으며,

Δ y = sin φ sin ζ + cos φ cos ζ cos (α − G H A − λ) − sin E l

(9)

i번째 측정값에 대한 민감도 행렬 A_i는 아래와 같이 계산할 수 있다.

A i = [cos φ sin ζ i − sin φ cos ζ i cos (α − G H A − λ) cos φ cos ζ i sin (α i − G H A − λ)] T

(10)

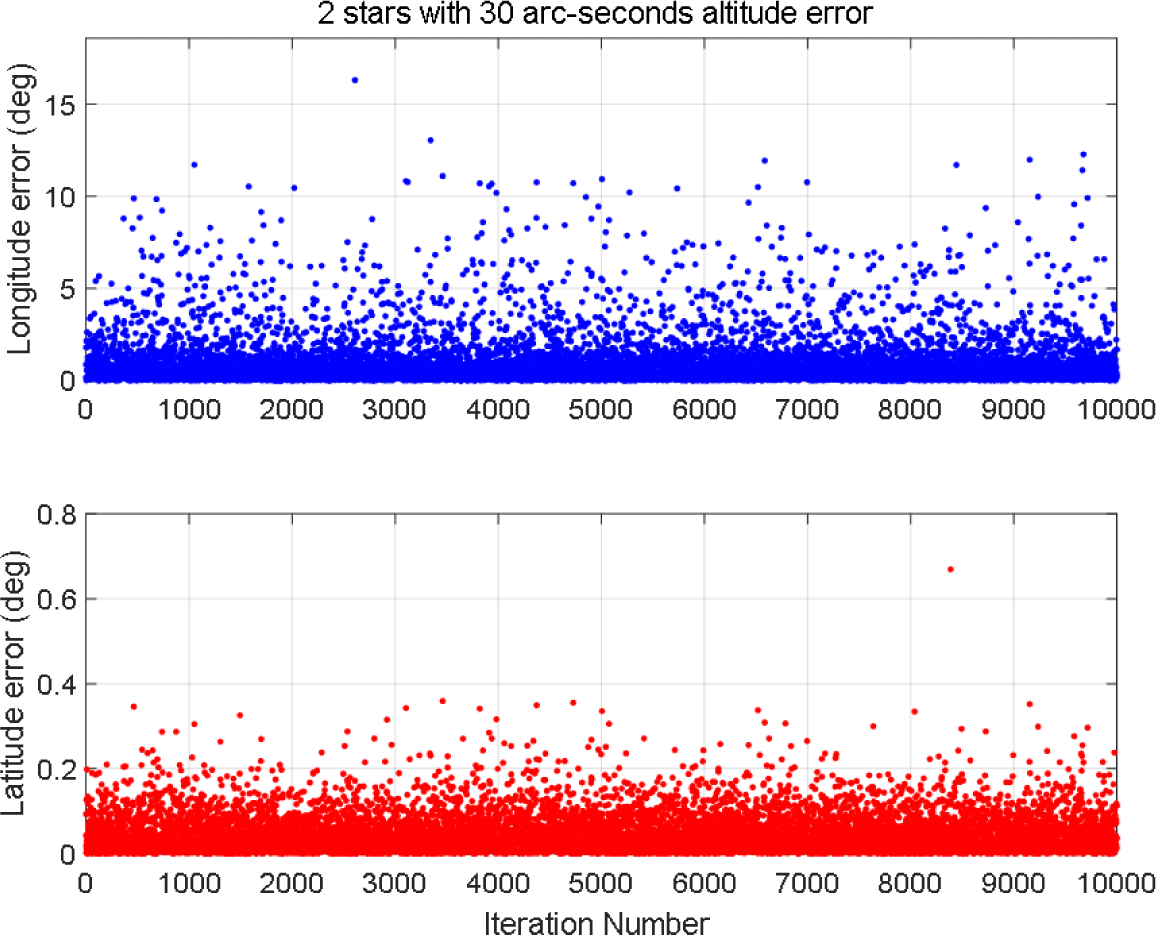
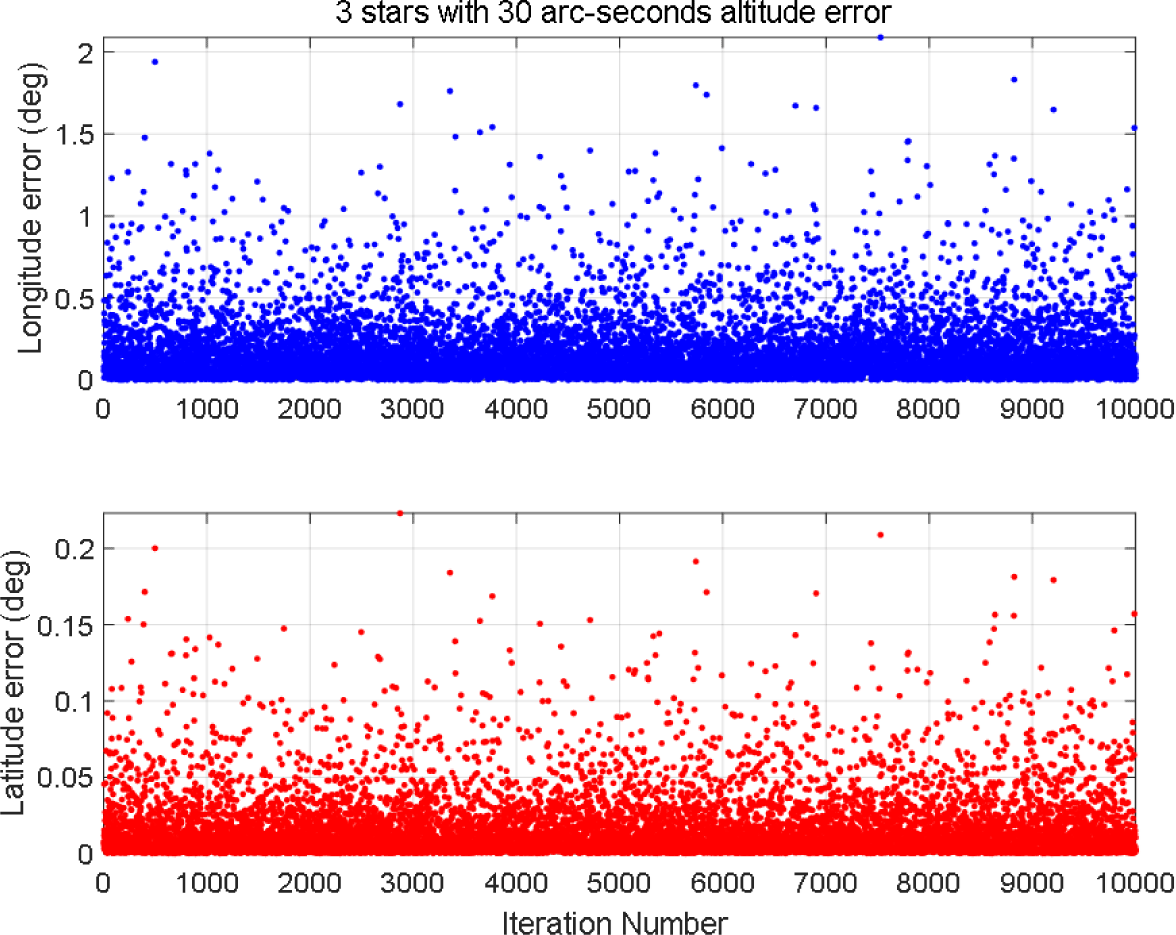
천측 항법에 대한 수평 위치 계산 결과는 시뮬레이션을 통해 확인해 보았다. 먼저 별의 고도를 30 arc-second(1σ)의 정확도로 측정하는 것을 가정하였으며, 사용된 별의 개수는 2개 및 3개로 차이를 두어 시뮬레이션을 수행하였다. 관측자의 위치는 매 시뮬레이션마다 위도 [-2/π, 2/π], 경도는 [-π, π] 사이의 임의의 값으로 생성하여 총 10,000회 수행하였다. 시뮬레이션 결과는 Figs. 3, 4와 같으며 각각 별의 개수가 2, 3개인 경우의 결과를 도시한다.

Fig. 3. Position errors of celestial navigation with 2 stars.

Download Original Figure

Fig. 4. Position errors of celestial navigation with 3 stars.

Download Original Figure

시뮬레이션 결과를 통해 별의 개수가 증가할수록 위치 추정에 대한 정확도가 증가하는 것을 알 수 있으며, 2개의 별을 사용한 경우에는 오차가 매우 커서 항법 시스템에 사용하기에는 무리가 있는 것을 확인할 수 있다. 따라서 최소자승법을 통해 위치를 결정하는 경우 적어도 3개 이상의 측정값이 있어야 함을 알 수 있다. 또한 민감도 행렬에 따라 위도보다는 상대적으로 모호성이 큰 경도에 대한 오차가 큰 것을 확인할 수 있다.

3. 항법시스템 설계

항법 시스템 설계를 위해서는 먼저 항법해가 표현될 기준 좌표계를 설정하는 것이 필수적이다. 본 논문에서는 천측 항법의 위치 추정값 활용이 용이하도록 지면좌표계(North East Down, NED)를 기준 좌표계로 사용하였다. 아래는 지면좌표계에서 표현된 관성측정장치의 지배 방정식(governing equation)을 나타낸다. 관성측정장치를 구성하는 각속도계 및 가속도계의 장착각 및 scale factor 오차 등은 고려하지 않고 바이어스(bias)만을 이용하여 모델링하였다.

q ˙ = 12 Ξ (q) ω B / N B

(11)

ω B / N B = (ω ˜ B / I B − b g − η v) − C N B (q) ω N / I N

(12)

φ ˙ = V N (R φ + h)

(13)

λ ˙ = V E (R λ + h) c o s φ

(14)

h ˙ = − v D

(15)

v ˙ N = − [V E (R λ + h) c o s φ + 2 ω e] v E s i n φ + v N v D R φ + h + a N

(16)

v ˙ E = [V E (R λ + h) c o s φ + 2 ω e] v N s i n φ + v E v D R λ + h + 2 ω e v D c o s φ + a E

(17)

v ˙ D = − v E 2 R λ + h − v N 2 R φ + h − 2 ω e v E c o s φ + g + a D

(18)

a B = (a ˜ B − b a − η av)

(19)

b ˙ g = η gu

(20)

b ˙ a = η au

(21)

여기서 q, φ, λ, h는 각각 비행체의 자세, 위도, 경도, 고도를 의미하며, v_N, v_E, v_D는 각각 NED 방향으로의 속도, 그리고 b_g 및 b_a는 각속도계와 가속도계의 바이어스를 의미한다.

항법해를 추정하기 위하여 일반적인 확장칼만필터(Extended Kalman Filter)를 사용하였다. 상태변수는 자세, 위치, 속도, 각속도계와 가속도계의 바이어스로 구성되며, 아래와 같이 행렬의 형태로 표현이 가능하다.

x = [q p v N b g b a], Δ x = [δ ϕ Δ p Δ v N Δ b g Δ b a], w = [η gv η gu η av η au]

(22)

실제 추정을 위한 상태 천이 방정식은 추정값과 실제값과의 차이를 나타내는 오차인 ∆x에 대한 방정식으로 표현되며 행렬 F와 G는 [8]에 나온 식을 참고하였다.

Δ x ˙ = FΔx + Gw

(23)

앞의 절에서 설명했지만 천측 항법은 기본적으로 위도 및 경도에 대한 정보만을 제공하기 때문에 자세에 대한 정보를 획득할 수 있는 별 센서 및 고도계의 사용이 필요하다. 측정값을 통해 상태변수를 올바르게 추정하기 위해서는 측정값과 상태변수 사이의 관계를 나타내는 민감도(sensitivity) 행렬을 정의해야 한다. 따라서 관성측정장치를 보정하기 위한 별 센서, 천측 항법, 고도계의 3가지 측정값에 대한 민감도 행렬을 정의한다.

먼저 별 센서의 측정값은 동체의 관성좌표계에 대한 자세변환행렬로 $C I B$ 로 표현할 수 있다. 여기서 B와 I는 동체 프레임과 관성 프레임을 의미한다. 센서로부터 획득한 $C I B$ 는 아래와 같이 연속적인 자세변환으로 표현될 수 있다.

C I B = C N B C E N C I E

(24)

항법해로부터 추정된 값은 자세와 위치 추정 오차를 포함하고 있기 때문에 다음과 같이 나타낼 수 있다.

C ˜ I B = (I − [α ×]) C N B (q^) (I + [δ p ×]) C E N (p^) C I E

(25)

C ˜ I B = (I − [α ×]) (I − [δ p ×]) C^I B

(26)

식의 양변에 $C^B I$ 를 곱한 후 정리하면 다음과 같다.

C ˜ I B C^B I = (I − [α ×]) (I − [δ p ×]) = I − [α ×] − [δ p ×]

(27)

이 때, 별 센서의 측정값 z_ST는 다음과 같이 정리할 수 있다.

z S T = I − C ˜ I B C^B I = [α ×] + [δ p ×]

(28)

따라서 별 센서 측정값의 민감도 행렬 H_ST 는 아래와 같다.

H S T = [I 3 × 3, H δ p, S T, 0 3 × 9]

(29)

H δ p, S T = [0 cos φ 0 − 1 00 0 − sin φ 0]

(30)

앞서 식에서 표현된 H_δp,ST는 자세 측정값과 위치 오차 사이의 관계를 의미한다. 지면좌표계에서 위치에 대한 오차 모델 δp는 $C E N$ 으로부터 유도할 수 있다.

C^E N = C E N + Δ C E N = [I − [δ p ×]] C E N

(31)

위 식에서 다음의 식을 정리할 수 있다.

Δ C E N = − [δ p ×] C E N

(32)

지면고정좌표계를 나타내는 E프레임에서 지면좌표계 N프레임으로의 변환 행렬은 아래와 같이 정의된다.

C E N = [− s i n φ c o s λ − s i n λ − cos φ c o s λ − sin φ s i n λ c o s λ − cos φ s i n λ c o s φ 0 − s i n φ]

(33)

이 때 위치 오차를 포함한 식은 아래와 같다.

C^E N = [− sin (φ + δ φ) cos (λ + δ λ) − sin (λ + δ λ) − cos (φ + δ φ) cos (λ + δ λ) − sin (φ + δ φ) sin (λ + δ λ) cos (λ + δ λ) − cos (φ + δ φ) sin (λ + δ λ) cos (φ + δ φ) 0 − sin (φ + δ φ)]

(34)

위 식을 전개하여 정리하면 아래와 같다.

C^E N = [0 sin φ δ λ − δ φ − sin φ δ λ 0 − cos φ δ λ δ φ cos φ δ λ 0] [− s i n φ c o s λ − s i n λ − cos φ c o s λ − sin φ s i n λ c o s λ − cos φ s i n λ c o s φ 0 − s i n φ]

(35)

따라서 δp는 아래의 식과 같으며, 해당 식을 [δφ, δλ, δh]에 대해서 미분할 경우 H_δp,ST 식을 획득할 수 있다.

[δ p ×] = [[cos φ δ λ − δ φ − sin φ δ λ] ×]

(36)

다음으로 천측 항법의 측정값에 대한 민감도 행렬을 정의한다. 약결합 방식은 천측 항법 내에서 별의 고도를 활용하여 수평 위치, 즉 상태변수와 동일한 위도와 경도를 항법 시스템에 제공하는 경우를 의미한다. 이 경우 천측 항법만으로도 위치를 알 수 있다는 장점이 있지만, 위치를 알아내기 위하여 다수의 측정값이 필요하므로 만일 2개 이하의 측정값이 들어오는 경우 올바른 위치를 제공하지 못하여 오차를 보정하지 못할 가능성도 있다.

강결합 방식의 경우, 별의 고도 측정값을 바로 항법 시스템에 제공하는 방법으로 시스템의 복잡성은 올라가지만 천측 항법의 수렴과 무관하게 항법 시스템에서 위치에 대한 정보 획득에 활용 가능하다는 장점이 있다. 약결합과 강결합은 측정값의 형태가 다르므로 서로 다른 민감도 행렬을 가지게 된다. 아래는 약결합 방식의 민감도 행렬을 나타낸다.

H C N S_l o o s e l y = [0 2 × 3, I 2 × 2, 0 2 × 10]

(37)

본 논문에서 제시하는 강결합 방식은 LOP 식을 측정값으로 활용한다. 이를 위하여 앞서 소개한 LOP 식과 위치 추정 오차와의 관계를 유도해야 한다.

s i n E l ˜ = sin (φ + δφ) sinζ + cos (φ + δφ) c o s ζcos (α − G H A − λ − δ λ)

(38)

s i n E l ˜ = sin El^+ [c o s φsinζ − sinφcosζcos (α − G H A − δ λ)] δφ + [cosφcosζsin (α − G H A − δ λ)] δ λ

(39)

따라서, 강결합 방식의 측정값 및 민감도 행렬은 아래와 같으며 i와 N은 i번째 측정값과 측정값의 개수를 각각 의미한다.

z C N S_t i g h t l y = s i n E l ˜ i − sin (φ^) sinζ i + cos (φ^) c o s ζ i cos (α i − G H A − λ^)

(40)

H C N S, t i g h t l y = [0 N × 3, H δφ i, H δ λ i, 0 N × 10]

(41)

H δ φ i = cos φ^sin ς i − sin φ^cos ς i cos (α i − G H A − λ^)

(42)

H δ λ i = cos φ^cos ς i sin (α i − G H A − λ^)

(43)

마지막으로 고도계로부터 획득한 고도 측정값에 대한 민감도 행렬은 다음과 같다.

H a l t = [0 1 × 5, 1, 0 1 × 9]

(44)

최종적으로 항법 시스템에 사용되는 민감도 행렬은 아래와 같다. 천측 항법의 민감도 행렬은 약결합 혹은 강결합 방식에 따라 변경된다.

H m e a s = [H S T H C N S_t i g h t l y H a l t]

(45)

제시한 항법 시스템은 Table 1과 같이 정리할 수 있다.

Table 1. Overall algorithm of proposed navigation system with celestial navigation

<Propagation Step>

- Attitude

ω B / N B = (ω ˜ B / I B − b g − η v) − C N B (q) ω N / I N

q ˙ = 12 Ξ (q) ω B / N B

- Position and velocity

φ ˙ = V N (R φ + h), λ ˙ = V E (R λ + h) c o s φ, h ˙ = − v D

v ˙ N = − [V E (R λ + h) c o s φ + 2 ω e] v E s i n φ + v N v D R φ + h + a N

v ˙ E = [V E (R λ + h) c o s φ + 2 ω e] v N s i n φ + v E v D R λ + h + 2 ω e v D c o s φ + a E

v ˙ D = − v E 2 R λ + h − v N 2 R φ + h − 2 ω e v E c o s φ + g + a D

- Covariance matrix

P ˙ (t) = F [x^(t), t] P (t) + P (t) F T [x^(t), t] + G (t) Q (t) G T (t)

<Update Step From Each Sensor>

- Sensitivity matrix of star sensor

H S T = [I 3 × 3, H δ p, S T, 0 3 × 9]

- Sensitivity matrix of altimeter

H a l t = [0 1 × 5, 1, 0 1 × 9]

- Sensitivity matrix of celestial navigation

- FOR i = 1:N

H i C N S_t i g h t l y = [0 N × 3, H δ φ, H δ λ, 0 N × 10]

END FOR

H = [H S T, H a l t, H C N S] T

- Gain calculation

K k = P k − H T (x^k −) [H P k − H T (x^k −) + R] − 1

P k + = [I − K k H T (x^k −)] P k −

- Final update

Δ x^k + = K k [z ˜ − H (x^k −)]

x^k + = x^k − + Δ x^k +

Download Excel Table

4. 시뮬레이션 결과

시뮬레이션에서는 설계한 항법 시스템이 올바르게 상태변수들을 추정하는지 확인해본다. 이를 위하여 사용되는 센서들의 성능은 다음과 같이 정의하였다. 별 센서는 10 arc-second(1σ)의 정확도와 10 Hz의 업데이트 속도를 가정하였다. 천측 항법의 경우 약결합 방식에서는 별의 고도로부터 위도와 경도를 최소자승법을 통해 계산하여 항법 시스템에 제공하며, 강결합의 경우 별의 고도를 그대로 항법 시스템에 제공하여 LOP 식을 측정값으로 사용할 수 있도록 하였다. 따라서 천측 항법의 수렴을 위하여 3개의 별의 고도를 30 arc-second(1σ)의 정확도로 측정하는 것을 가정하였으며, 별 센서와 동일하게 10 Hz의 업데이트 속도를 가정하였다. 마지막으로 고도계는 1 Hz의 업데이트 속도와 함께 고도 참값의 1%(1σ) 오차를 가진다고 가정하였다.

시뮬레이션에서 사용된 관성측정장치의 성능 및 초기 오차는 Table 2 및 Table 3에 정리하였으며, 시뮬레이션은 총 1,000초 진행하였다.

Table 2. Specification of inertial measurement units

	Inertial measurement unit
	Gyroscope	Accelerometer
Update rate	50 Hz
Random noise	0.005 deg/rhr	17 μg/rHz
Bias	0.01 deg/hr	30 μg
Bias drift	0.005 deg/hr	30 μg/hr

Download Excel Table

Table 3. Initial errors for simulation study

	Initial error
Attitude	[0.1deg −0.1deg 0.1deg]
Position	[−0.01deg 0.01deg 50m]
Velocity	[−5m/s 5m/s 5m/s]

Download Excel Table

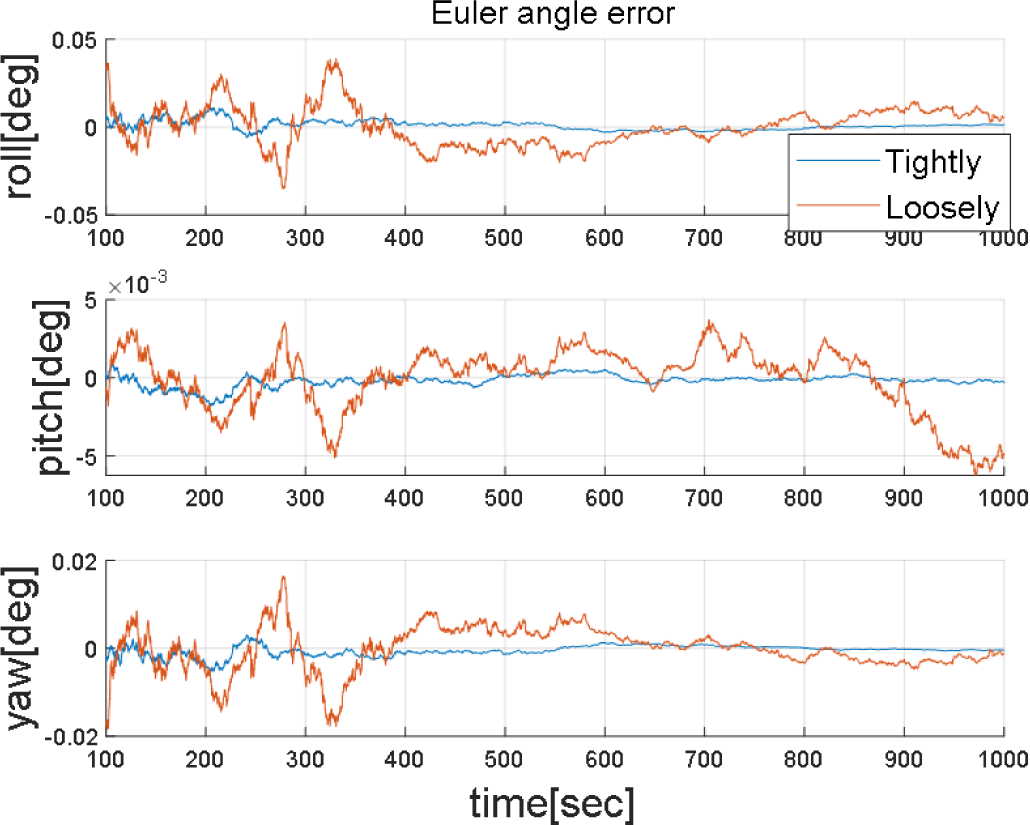
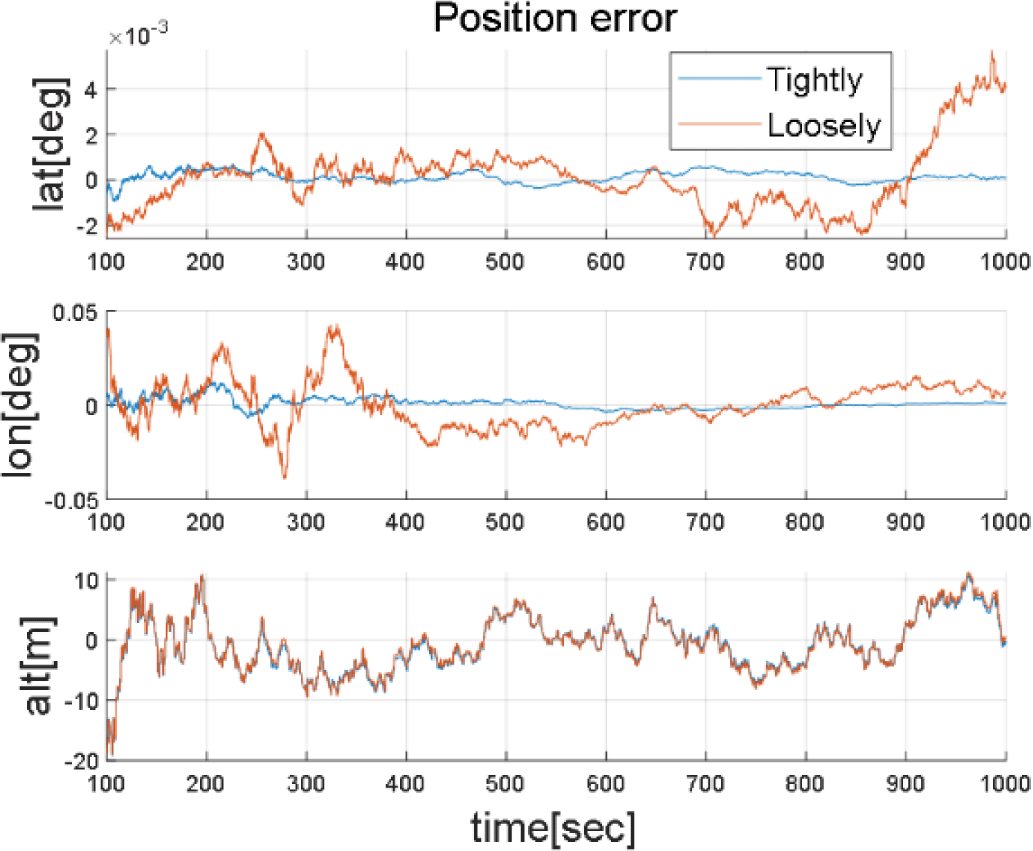
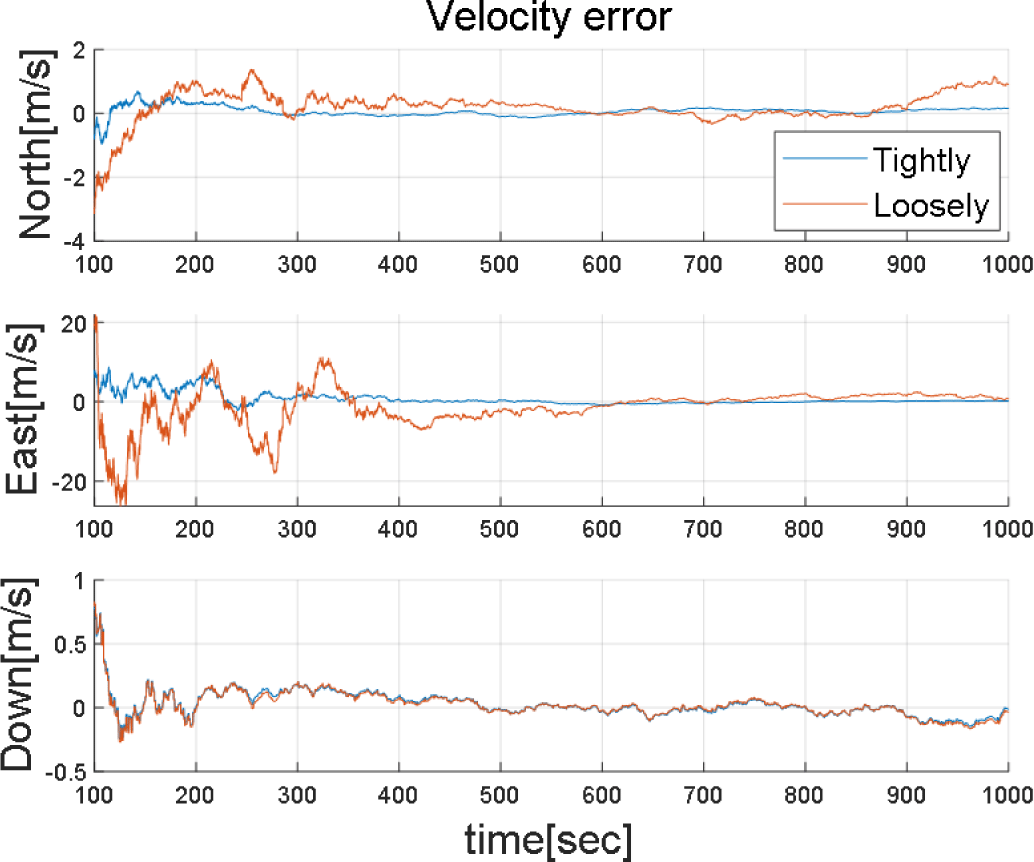
설계된 약결합 및 강결합 방식의 비교 결과를 Figs. 5-7에 도시하였으며, 강결합 및 약결합은 각각 파랑색과 주황색으로 나타냈다.

Fig. 5. The attitude errors of proposed navigation system.

Download Original Figure

Fig. 6. The position errors of proposed navigation system.

Download Original Figure

Fig. 7. The velocity errors of proposed navigation system.

Download Original Figure

시뮬레이션 결과를 통해 약결합 및 강결합의 두 방식 모두 수평 위치를 올바르게 추정하는 것을 알 수 있으며, 강결합 방식의 항법 시스템이 시간이 지남에 따라 더욱 안정적으로 항법 해를 추정하는 것을 확인할 수 있다. 약결합 방식은 천측 항법에서 추정된 오차에 따라 항법 해의 정확도가 좌우되는데 최소자승법을 활용할 경우 시간과 관계 없이 그 오차 수준이 일정하기 때문에 시간에 따른 정확도는 좋아지지 않는다.

이러한 결과를 바탕으로 약결합 방식과 같이 천측 항법에서 수평 위치를 제공하는 방식은 항법 시스템의 초기화 단계에서 사용되는 것이 효율적으로 판단되며, 이후에는 강결합 방식의 항법 시스템을 활용하는 것이 좋을 것으로 판단된다. 또한 강결합 방식은 약결합 방식과 달리 고도에 대한 측정값이 1개인 경우에도 수평 위치의 추정이 가능하다는 장점을 가지고 있다. Table 4는 두 방식의 평균 제곱근 오차를 정리하였다.

Table 4. Root mean square errors according to coupled methods

	Tightly-coupled	Loosely-coupled
Attitude (deg)	1.8495e-3	0.0185
	3.7954e-4	0.0031
	9.2055e-4	0.0077
Position (deg)	2.9402e-4	0.0012
Position (deg)	2.0972e-3	0.0203
Altitude (m)	5.7835	5.9802
Velocity (m/s)	0.1812	0.3516
	1.2345	6.8257
	0.1022	0.1075

Download Excel Table

5. 결론

본 논문에서는 천측 항법을 활용한 항법 시스템에 대하여 기술하였다. 특히 심우주 탐사에 대한 임무가 많아지면서 단독적인 항법 시스템을 구현할 수 있는 관성 항법과 천측 항법을 동시에 활용할 수 있는 방안을 제시하였다. 천측 항법이 제공할 수 있는 정보는 수평 위치로써 제공하는 형태에 따라 약결합과 강결합으로 나뉠 수 있다. 그 중에서도 LOP 식을 활용한 강결합 형태의 항법 시스템을 제시하고 시뮬레이션을 통한 결과를 확인해 보았다. 수평 위치를 직접적으로 획득할 수 있는 약결합 방식의 경우 항법 해의 초기화에 장점이 있지만, 강결합 방식은 측정값의 개수와 관계없이 시간에 지남에 따라 더욱 안정적으로 항법 해를 추정할 수 있었다. 따라서 두 방식의 장단점을 고려한다면 향후 임무 및 항법 시스템의 목적에 따라 올바른 항법 시스템을 설계하는 데 도움이 될 것으로 사료된다.

감사의 글

본 연구는 한국항공우주연구원의 자체적으로 수행 중인 '아포피스(소행성) 탐사 기초연구' 연구의 일부이며, 지원에 감사드린다.

References

Ning X, Gui M, Xu Y, Bai X, Fang J, INS/VNS/CNS integrated navigation method for planetary rovers, Aerosp. Sci. Technol. 48, 102-114 (2015).

Barshan B, Durrant-Whyte HF, Inertial navigation systems for mobile robots, IEEE Trans. Robot. Autom. 11, 328-342 (1995).

Ning X, Liu L, A two-mode INS/CNS navigation method for lunar rovers, IEEE Trans. Instrum. Meas. 63, 2170-2179 (2014).

Yang Y, Zhang C, Lu J, Zhang H, Classification of methods in the SINS/CNS integration navigation system, IEEE Access 6, 3149-3158 (2018).

Yang L, Li B, Ge L, A novel SINS/CNS integrated navigation algorithm used in a ballistic missile, Int. J. Sec. Appl. 9, 65-76 (2015).

Tsou MC, Genetic algorithm for solving celestial navigation fix problems, Pol. Marit. Res. 19, 53-59 (2012).

Pierros F, Stand-alone celestial navigation positioning method, J. Navig. 71, 1-19 (2018).

Crassidis JL, Junkins JL, Optimal Estimation of Dynamic Systems (Chapman and Hall, New York, NY, 2004).

Author Information

김 기 덕KiduckKim@kari.re.kr

jsta-3-1-58-i1

KAIST에서 2013, 2015, 2020년 학사, 석사, 박사 학위를 취득하고, 2020년부터 한국항공우주연구원에서 선임연구원으로 재직 중이다. 현재 랑데부/도킹 기술 개발을 하고 있다.

수평 위치정보 추정을 위한 관성/천측 항법시스템 설계 및 약결합/강결합 방식의 성능 비교

요 약

Abstract

1. 서론

2. 천측 항법(Celestial Navigation)

3. 항법시스템 설계

4. 시뮬레이션 결과

5. 결론

감사의 글

References

Author Information

2023년 한국연구재단 등재후보학술지 선정